
The rainbow effect is also commonly seen near waterfalls or fountains. In addition, the effect can be artificially created by dispersing water droplets into the air during a sunny day. Rarely, a moonbow, lunar rainbow or nighttime rainbow, can be seen on strongly moonlit nights. As human visual perception for colour is poor in low light, moonbows are often perceived to be white.
It is difficult to photograph the complete semicircle of a rainbow in one frame, as this would require an angle of view of 84°. For a 35 mm camera, a wide-angle lens with a focal length of 19 mm or less would be required. Now that software for stitching several images into a panorama is available, images of the entire arc and even secondary arcs can be created fairly easily from a series of overlapping frames.
From above the earth such as in an aeroplane, it is sometimes possible to see a rainbow as a full circle. This phenomenon can be confused with the glory phenomenon, but a glory is usually much smaller, covering only 5–20°.
The sky inside a primary rainbow is brighter than the sky outside of the bow. This is because each raindrop is a sphere and it scatters light over an entire circular disc in the sky. The radius of the disc depends on the wavelength of light, with red light being scattered over a larger angle than blue light. Over most of the disc, scattered light at all wavelengths overlaps, resulting in white light which brightens the sky. At the edge, the wavelength dependence of the scattering gives rise to the rainbow.
Light of primary rainbow arc is 96% polarised tangential to the arch. Light of second arc is 90% polarised.
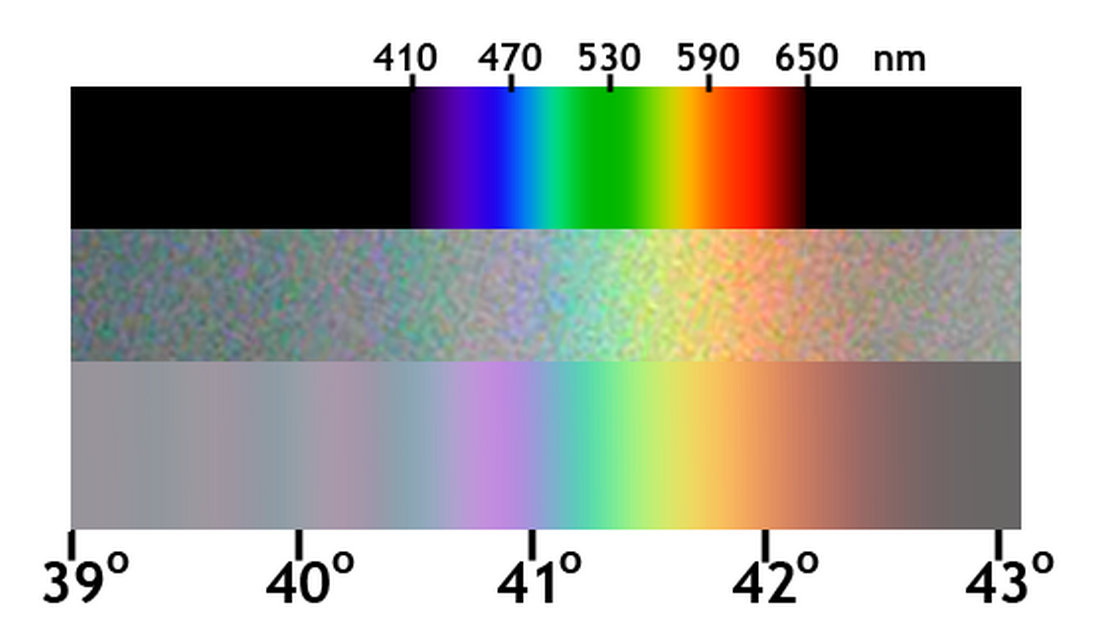
Number of colours in spectrum or rainbow
A spectrum obtained using a glass prism and a point source is a continuum of wavelengths without bands. The number of colours that the human eye is able to distinguish in a spectrum is in the order of 100. Accordingly, the Munsell colour system (a 20th-century system for numerically describing colours, based on equal steps for human visual perception) distinguishes 100 hues. The apparent discreteness of main colours is an artefact of human perception and the exact number of main colours is a somewhat arbitrary choice.
Red Orange Yellow Green Blue Indigo Violet
Newton, who admitted his eyes were not very critical in distinguishing colours, originally (1672) divided the spectrum into five main colours: red, yellow, green, blue and violet. Later he included orange and indigo, giving seven main colours by analogy to the number of notes in a musical scale. Newton chose to divide the visible spectrum into seven colours out of a belief derived from the beliefs of the ancient Greek sophists, who thought there was a connection between the colours, the musical notes, the known objects in the Solar System, and the days of the week.
According to Isaac Asimov, “It is customary to list indigo as a color lying between blue and violet, but it has never seemed to me that indigo is worth the dignity of being considered a separate color. To my eyes it seems merely deep blue.”
The colour pattern of a rainbow is different from a spectrum, and the colours are less saturated. There is spectral smearing in a rainbow owing to the fact that for any particular wavelength, there is a distribution of exit angles, rather than a single unvarying angle. In addition, a rainbow is a blurred version of the bow obtained from a point source, because the disk diameter of the sun (0.5°) cannot be neglected compared to the width of a rainbow (2°). The number of colour bands of a rainbow may therefore be different from the number of bands in a spectrum, especially if the droplets are particularly large or small. Therefore, the number of colours of a rainbow is variable. If, however, the word rainbow is used inaccurately to mean spectrum, it is the number of main colours in the spectrum.
The question of whether everyone sees seven colours in a rainbow is related to the idea of Linguistic relativity. Suggestions have been made that there is universality in the way that a rainbow is perceived. However, more recent research suggests that the number of distinct colours observed and what these are called depend on the language that one uses with people whose language has fewer colour words seeing fewer discrete colour bands.
Explanation
The reason the returning light is most intense at about 42° is that this is a turning point – light hitting the outermost ring of the drop gets returned at less than 42°, as does the light hitting the drop nearer to its centre. There is a circular band of light that all gets returned right around 42°. If the sun were a laser emitting parallel, monochromatic rays, then the luminance (brightness) of the bow would tend toward infinity at this angle (ignoring interference effects). (See Caustic (optics).) But since the sun’s luminance is finite and its rays are not all parallel (it covers about half a degree of the sky) the luminance does not go to infinity. Furthermore, the amount by which light is refracted depends upon its wavelength, and hence its colour. This effect is called dispersion. Blue light (shorter wavelength) is refracted at a greater angle than red light, but due to the reflection of light rays from the back of the droplet, the blue light emerges from the droplet at a smaller angle to the original incident white light ray than the red light. Due to this angle, blue is seen on the inside of the arc of the primary rainbow, and red on the outside. The result of this is not only to give different colours to different parts of the rainbow, but also to diminish the brightness. (A “rainbow” formed by droplets of a liquid with no dispersion would be white, but brighter than a normal rainbow.)
Light rays enter a raindrop from one direction (typically a straight line from the sun), reflect off the back of the raindrop, and fan out as they leave the raindrop. The light leaving the rainbow is spread over a wide angle, with a maximum intensity at the angles 40.89–42°. (Note: Between 2 and 100% of the light is reflected at each of the three surfaces encountered, depending on the angle of incidence. This diagram only shows the paths relevant to the rainbow.)
White light separates into different colours on entering the raindrop due to dispersion, causing red light to be refracted less than blue light.
When sunlight encounters a raindrop, part of the light is reflected and the rest enters the raindrop. The light is refracted at the surface of the raindrop. When this light hits the back of the raindrop, some of it is reflected off the back. When the internally reflected light reaches the surface again, once more some is internally reflected and some is refracted as it exits the drop. (The light that reflects off the drop, exits from the back, or continues to bounce around inside the drop after the second encounter with the surface, is not relevant to the formation of the primary rainbow.) The overall effect is that part of the incoming light is reflected back over the range of 0° to 42°, with the most intense light at 42°. This angle is independent of the size of the drop, but does depend on its refractive index. Seawater has a higher refractive index than rain water, so the radius of a “rainbow” in sea spray is smaller than a true rainbow. This is visible to the naked eye by a misalignment of these bows.
The light at the back of the raindrop does not undergo total internal reflection, and some light does emerge from the back. However, light coming out the back of the raindrop does not create a rainbow between the observer and the sun because spectra emitted from the back of the raindrop do not have a maximum of intensity, as the other visible rainbows do, and thus the colours blend together rather than forming a rainbow.
A rainbow does not exist at one particular location. Many rainbows exist; however, only one can be seen depending on the particular observer’s viewpoint as droplets of light illuminated by the sun. All raindrops refract and reflect the sunlight in the same way, but only the light from some raindrops reaches the observer’s eye. This light is what constitutes the rainbow for that observer. The whole system composed by the sun’s rays, the observer’s head, and the (spherical) water drops has an axial symmetry around the axis through the observer’s head and parallel to the sun’s rays. The rainbow is curved because the set of all the raindrops that have the right angle between the observer, the drop, and the sun, lie on a cone pointing at the sun with the observer at the tip. The base of the cone forms a circle at an angle of 40–42° to the line between the observer’s head and their shadow but 50% or more of the circle is below the horizon, unless the observer is sufficiently far above the earth’s surface to see it all, for example in an aeroplane. Alternatively, an observer with the right vantage point may see the full circle in a fountain or waterfall spray.
Mathematical derivation
We can determine the perceived angle which the rainbow subtends as follows.
Given a spherical raindrop, and defining the perceived angle of the rainbow as 2φ, and the angle of the internal reflection as 2β, then the angle of incidence of the sun’s rays with respect to the drop’s surface normal is 2β − φ. Since the angle of refraction is β, Snell’s law gives us
sin(2β − φ) = n sin β,
where n = 1.333 is the refractive index of water. Solving for φ, we get
φ = 2β − arcsin(n sin β).
The rainbow will occur where the angle φ is maximum with respect to the angle β. Therefore, from calculus, we can set dφ/dβ = 0, and solve for β, which yields
Substituting back into the earlier equation for φ yields 2φmax ≈ 42° as the radius angle of the rainbow.
Source From Wikipedia