Cinemática de partículas

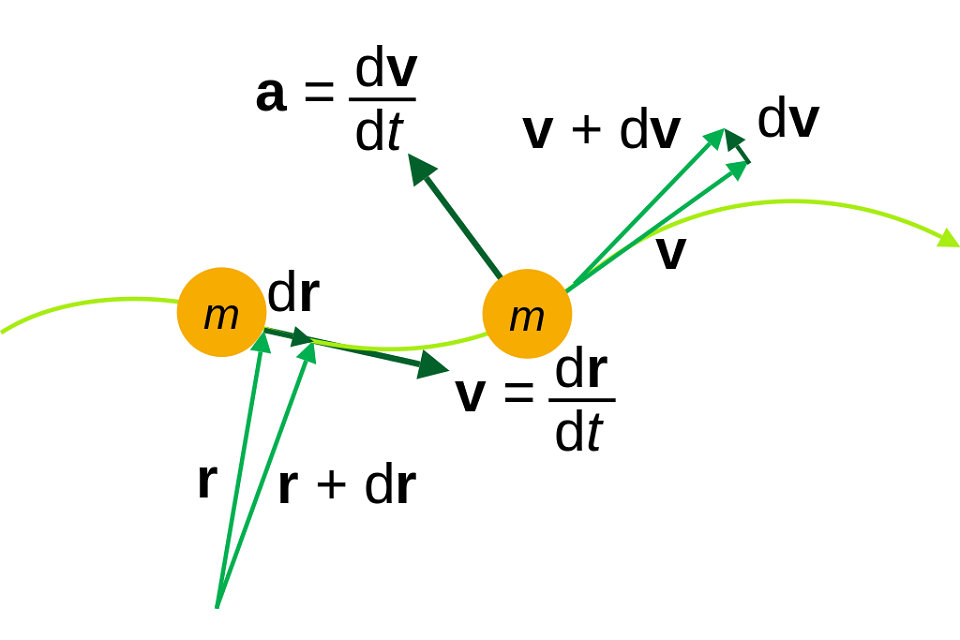
La cinemática de partículas es el estudio de la trayectoria de una partícula. La posición de una partícula se define como el vector de coordenadas desde el origen de un marco de coordenadas a la partícula.

Cinemática de una trayectoria de partículas en un marco de referencia no giratorio
En el caso más general, se utiliza un sistema de coordenadas tridimensional para definir la posición de una partícula. Sin embargo, si la partícula está limitada a moverse en una superficie, un sistema de coordenadas bidimensional es suficiente. Todas las observaciones en física están incompletas sin que esas observaciones se describan con respecto a un marco de referencia.

El vector de posición de una partícula es un vector dibujado desde el origen del marco de referencia a la partícula. Expresa tanto la distancia del punto desde el origen como su dirección desde el origen. En tres dimensiones, la posición del punto P se puede expresar como 

dónde  ,  y  son las coordenadas cartesianas y  ,  y  son los vectores unitarios a lo largo del  ,  y  ejes de coordenadas, respectivamente. La magnitud del vector de posición.  da la distancia entre el punto  y el origen.

Los cosenos de dirección del vector de posición proporcionan una medida cuantitativa de la dirección. Es importante tener en cuenta que el vector de posición de una partícula no es único. El vector de posición de una partícula dada es diferente en relación con diferentes marcos de referencia.

La trayectoria de una partícula es una función vectorial del tiempo.  , que define la curva trazada por la partícula en movimiento, dada por 
donde las coordenadas x _P , y _P yz _P son funciones del tiempo.

Velocidad y velocidad
La velocidad de una partícula es una cantidad vectorial que describe la dirección del movimiento y la magnitud del movimiento de la partícula. Más matemáticamente, la velocidad de cambio del vector de posición de un punto, con respecto al tiempo, es la velocidad del punto. Considere la relación formada dividiendo la diferencia de dos posiciones de una partícula por el intervalo de tiempo. Esta relación se denomina velocidad promedio durante ese intervalo de tiempo y se define como Velocidad = desplazamiento / tiempo tomado

donde ΔP es el cambio en el vector de posición durante el intervalo de tiempo Δt.
En el límite a medida que el intervalo de tiempo Δt se hace cada vez más pequeño, la velocidad promedio se convierte en la derivada temporal del vector de posición, 

La velocidad de un objeto es la magnitud | V | de su velocidad. Es una cantidad escalar:

donde s es la longitud del arco medida a lo largo de la trayectoria de la partícula. Esta longitud de arco recorrida por una partícula en el tiempo es una cantidad no decreciente. Por lo tanto, ds / dt no es negativo, lo que implica que la velocidad tampoco es negativa.

Aceleración
El vector de velocidad puede cambiar en magnitud y en dirección o ambos a la vez. Por lo tanto, la aceleración es la tasa de cambio de la magnitud del vector de velocidad más la tasa de cambio de dirección de ese vector. El mismo razonamiento utilizado con respecto a la posición de una partícula para definir la velocidad, se puede aplicar a la velocidad para definir la aceleración. La aceleración de una partícula es el vector definido por la velocidad de cambio del vector de velocidad. La aceleración media de una partícula en un intervalo de tiempo se define como la relación.

donde ΔV es la diferencia en el vector de velocidad y Δt es el intervalo de tiempo.
La aceleración de la partícula es el límite de la aceleración promedio a medida que el intervalo de tiempo se acerca a cero, que es la derivada del tiempo. 
o

La magnitud de la aceleración de un objeto es la magnitud | A | de su vector de aceleración. Es una cantidad escalar:

Vector de posicion relativa

Cuál es la diferencia entre los componentes de sus vectores de posición.

Si el punto B tiene componentes de posición 

entonces la posición del punto A en relación con el punto B es la diferencia entre sus componentes: 

Velocidad relativa
La velocidad de un punto en relación con otro es simplemente la diferencia entre sus velocidades.

Cuál es la diferencia entre los componentes de sus velocidades.
Si el punto A tiene componentes de velocidad 
y el punto B tiene componentes de velocidad 

entonces la velocidad del punto A en relación con el punto B es la diferencia entre sus componentes: 
Alternativamente, este mismo resultado podría obtenerse calculando la derivada temporal del vector de posición relativa R _{B / A.}

En el caso de que la velocidad sea cercana a la velocidad de la luz c (generalmente dentro del 95%), otro esquema de velocidad relativa llamado velocidad, que depende de la relación de V a c, se usa en la relatividad especial.

Aceleración relativa
La aceleración de un punto C en relación con otro punto B es simplemente la diferencia entre sus aceleraciones.

Cuál es la diferencia entre los componentes de sus aceleraciones.
Si el punto C tiene componentes de aceleración. 
y el punto B tiene componentes de aceleración 

entonces la aceleración del punto C en relación con el punto B es la diferencia entre sus componentes: 
Alternativamente, este mismo resultado podría obtenerse calculando la segunda derivada del tiempo del vector de posición relativa P _{B / A.}

Trayectorias de partículas en constante aceleración.
Para el caso de aceleración constante, la ecuación diferencial Eq 1) se puede integrar ya que el vector de aceleración A de un punto P es constante en magnitud y dirección. Se dice que tal punto experimenta un movimiento uniformemente acelerado ^{. En este caso, la velocidad V (t) y luego la trayectoria P (t) de la partícula se pueden obtener integrando la ecuación de aceleración A con respecto al tiempo.}

Suponiendo que las condiciones iniciales de la posición,  , y la velocidad  en el momento  Como se sabe, la primera integración produce la velocidad de la partícula en función del tiempo.

Una segunda integración cede su trayectoria (trayectoria),

Se pueden derivar relaciones adicionales entre desplazamiento, velocidad, aceleración y tiempo.Dado que la aceleración es constante,  se puede sustituir en la ecuación anterior para dar:

Se puede tener una relación entre la velocidad, la posición y la aceleración sin una dependencia explícita del tiempo resolviendo la aceleración promedio por tiempo y sustituyendo y simplificando

donde ∘ denota el producto de puntos, que es apropiado ya que los productos son escalares en lugar de vectores.

El punto puede ser reemplazado por el coseno del ángulo.  entre los vectores ^{y los vectores por sus magnitudes, en cuyo caso:}

En el caso de la aceleración siempre en la dirección del movimiento, el ángulo entre los vectores (  ) es 0, entonces  y 

Esto se puede simplificar usando la notación para las magnitudes de los vectores.  ^{dónde  puede ser cualquier camino curvilíneo tomado como la constante aceleración tangencial se aplica a lo largo de ese camino , por lo que} 

Esto reduce las ecuaciones paramétricas de movimiento de la partícula a una relación cartesiana de velocidad frente a posición. Esta relación es útil cuando el tiempo es desconocido. Tambien sabemos que  o  es el area debajo de av, t grafica. Podemos tomar  añadiendo el área superior y el área inferior. El área inferior es un rectángulo, y el área de un rectángulo es el rectángulo.  dónde  es el ancho y  es la altura. En este caso  y  (note que el  Aquí es diferente de la aceleración.  ). Esto significa que el área inferior es  . Ahora encontremos el área superior (un triángulo). El área de un trangle es  dónde  es la base y  es la altura.En este caso,  Y  o  . Añadiendo  y resultados en la ecuación  resultados en la ecuación  . Esta ecuación es muy útil cuando la velocidad final  es desconocido.

Trayectorias de partículas en coordenadas cilíndricas-polares.
A menudo es conveniente formular la trayectoria de una partícula P (t) = (X (t), Y (t) y Z (t)) usando coordenadas polares en el plano X – Y. En este caso, su velocidad y aceleración toman una forma conveniente.

Recuerde que la trayectoria de una partícula P se define por su vector de coordenadas P medido en un marco de referencia fijo F. A medida que la partícula se mueve, su vector de coordenadas P (t) traza su trayectoria, que es una curva en el espacio, dada por:

donde i, j y k son los vectores unitarios a lo largo de los ejes X, Y y Z del marco de referencia F, respectivamente.

Considere una partícula P que se mueve solo en la superficie de un cilindro circular R (t) = constante, es posible alinear el eje Z del marco fijo F con el eje del cilindro. Luego, el ángulo θ alrededor de este eje en el plano X – Y se puede usar para definir la trayectoria como, 

Las coordenadas cilíndricas para P (t) se pueden simplificar introduciendo los vectores de unidades radiales y tangenciales, 

y sus derivados del tiempo del cálculo elemental:



 .

Usando esta notación, P (t) toma la forma,

donde R es constante en el caso de que la partícula se mueva solo en la superficie de un cilindro de radio R.

En general, la trayectoria P (t) no está limitada a un cilindro circular, por lo que el radio R varía con el tiempo y la trayectoria de la partícula en coordenadas cilíndricas-polares se convierte en:

Donde R, theta y Z pueden ser funciones de tiempo continuamente diferenciables y la notación de función se descarta por simplicidad. El vector de velocidad V _P es la derivada temporal de la trayectoria P (t), que produce:  .

De manera similar, la aceleración A _P , que es la derivada en el tiempo de la velocidad V _P , viene dada por: 

El termino  Actúa hacia el centro de curvatura de la trayectoria en ese punto de la trayectoria, comúnmente se denomina aceleración centrípeta. El termino  Se llama la aceleración de Coriolis.

Radio constante
Si la trayectoria de la partícula está restringida a apoyarse en un cilindro, entonces el radio R es constante y los vectores de velocidad y aceleración se simplifican. La velocidad de V _P es la derivada temporal de la trayectoria P (t),

El vector de aceleración se convierte en:

Trayectorias circulares planares.
Un caso especial de una trayectoria de partículas en un cilindro circular ocurre cuando no hay movimiento a lo largo del eje Z:

donde R y Z ₀ son constantes. En este caso, la velocidad V _P viene dada por:

dónde

es la velocidad angular del vector unitario e _θ alrededor del eje z del cilindro.
La aceleración A _P de la partícula P ahora viene dada por:

Los componentes

Se llaman, respectivamente, los componentes radiales y tangenciales de la aceleración.
La notación para la velocidad angular y la aceleración angular se define a menudo como

por lo que los componentes de aceleración radial y tangencial para trayectorias circulares también se escriben como

Trayectorias puntuales en un cuerpo que se mueve en el plano.

Representación matricial
La combinación de una rotación y traslación en el plano R ² puede representarse por un cierto tipo de matriz 3×3 conocida como una transformada homogénea. La transformada homogénea de 3×3 se construye a partir de una matriz de rotación A (φ) de 2×2 y el vector de traslación 2×1 d = (d _x , d _y ), como: 

Estas transformaciones homogéneas realizan transformaciones rígidas en los puntos en el plano z = 1, es decir, en puntos con coordenadas p = (x, y, 1).

En particular, permita que p defina las coordenadas de los puntos en un marco de referencia M coincidente con un marco fijo F. Luego, cuando el origen de M se desplaza por el vector de traslación d con respecto al origen de Fand girado por el ángulo φ con respecto al En el eje x de F, las nuevas coordenadas en F de los puntos en M vienen dadas por:

Las transformaciones homogéneas representan transformaciones afines. Esta formulación es necesaria porque una traducción no es una transformación lineal de R ² . Sin embargo, al usar geometría proyectiva, de modo que R ² se considera un subconjunto de R ³ , las traducciones se convierten en transformaciones lineales afines.

Traducción pura
Si un cuerpo rígido se mueve para que su marco de referencia M no gire (∅ = 0) en relación con el marco fijo F, el movimiento se denomina traducción pura. En este caso, la trayectoria de cada punto en el cuerpo es un desplazamiento de la trayectoria d (t) del origen de M, es decir: 

Por lo tanto, para los cuerpos en traducción pura, la velocidad y la aceleración de cada punto P en el cuerpo vienen dadas por: 

donde el punto denota la derivada con respecto al tiempo y V _O y A _O son la velocidad y la aceleración, respectivamente, del origen del cuadro móvil M. Recuerde que el vector de coordenadas p en M es constante, por lo que su derivada es cero.

Rotación de un cuerpo alrededor de un eje fijo.
La cinemática rotacional o angular es la descripción de la rotación de un objeto. La descripción de la rotación requiere algún método para describir la orientación. Las descripciones comunes incluyen los ángulos de Euler y la cinemática de los giros inducidos por productos algebraicos.

En lo que sigue, la atención se limita a la rotación simple sobre un eje de orientación fija. El eje z ha sido elegido por conveniencia.

Posición
Esto permite la descripción de una rotación como la posición angular de un marco de referencia planar M con respecto a una F fija sobre este eje z compartido. Las coordenadas p = (x, y) en M están relacionadas con las coordenadas P = (X, Y) en F mediante la ecuación de matriz:

dónde

es la matriz de rotación que define la posición angular de M en relación con F en función del tiempo.

Velocidad
Si el punto p no se mueve en M, su velocidad en F viene dada por

Es conveniente eliminar las coordenadas p y escribir esto como una operación en la trayectoria P (t),

donde la matriz

se conoce como la matriz de velocidad angular de M con respecto a F. El parámetro ω es la derivada temporal del ángulo θ, es decir:

Aceleración
La aceleración de P (t) en F se obtiene como la derivada del tiempo de la velocidad,

que se convierte

dónde

es la matriz de aceleración angular de M en F, y

La descripción de la rotación implica estas tres cantidades:

Posición angular: la distancia orientada desde un origen seleccionado en el eje de rotación hasta un punto de un objeto es un vector r (t) que ubica el punto. El vector r (t) tiene alguna proyección (o, de manera equivalente, algún componente) r _⊥ (t) en un plano perpendicular al eje de rotación. Luego, la posición angular de ese punto es el ángulo θ desde un eje de referencia (típicamente el eje x positivo) al vector r _⊥ (t) en un sentido de rotación conocido (típicamente dado por la regla de la mano derecha).

Velocidad angular: la velocidad angular ω es la velocidad a la que la posición angular θ cambia con respecto al tiempo t:

La velocidad angular está representada en la Figura 1 por un vector Ω que apunta a lo largo del eje de rotación con magnitud ω y el sentido está determinado por la dirección de rotación dada por la regla de la mano derecha.

Aceleración angular: la magnitud de la aceleración angular α es la velocidad a la que la velocidad angular ω cambia con respecto al tiempo t:

Las ecuaciones de la cinemática traslacional pueden extenderse fácilmente a la cinemática rotacional plana para una aceleración angular constante con intercambios de variables simples:

Aquí θ _i y θ _f son, respectivamente, las posiciones angulares inicial y final, ω _i y ω _f son, respectivamente, las velocidades angulares inicial y final, y α es la aceleración angular constante.Aunque la posición en el espacio y la velocidad en el espacio son ambos vectores verdaderos (en términos de sus propiedades en rotación), al igual que la velocidad angular, el ángulo en sí no es un vector verdadero.

Trayectorias puntuales en cuerpo moviéndose en tres dimensiones.
Las fórmulas importantes en cinemática definen la velocidad y la aceleración de los puntos en un cuerpo en movimiento a medida que trazan trayectorias en el espacio tridimensional. Esto es particularmente importante para el centro de masa de un cuerpo, que se utiliza para derivar ecuaciones de movimiento utilizando la segunda ley de Newton o las ecuaciones de Lagrange.

Posición
Para definir estas fórmulas, el movimiento de un componente B de un sistema mecánico se define por el conjunto de rotaciones [A (t)] y las traducciones d (t) ensambladas en la transformación homogénea [T (t)] = [A (t), d (t)]. Si p es las coordenadas de un punto P en B medido en el marco de referencia móvil M, entonces la trayectoria de este punto trazado en F viene dada por: 

Esta notación no distingue entre P = (X, Y, Z, 1) y P = (X, Y, Z), lo que se espera que sea claro en el contexto.
Esta ecuación para la trayectoria de P se puede invertir para calcular el vector de coordenadas p en M como: 

Esta expresión utiliza el hecho de que la transposición de una matriz de rotación también es su inversa, es decir:

Velocidad
La velocidad del punto P a lo largo de su trayectoria P (t) se obtiene como la derivada temporal de este vector de posición, 

El punto denota la derivada con respecto al tiempo; Porque p es constante, su derivada es cero.

Esta fórmula se puede modificar para obtener la velocidad de P operando en su trayectoria P (t) medida en el marco fijo F. Sustituyendo la transformada inversa de p en los rendimientos de la ecuación de velocidad: 

La matriz [S] está dada por:

dónde

Es la matriz de velocidad angular.

Multiplicando por el operador [S], la fórmula para la velocidad V _P toma la forma:

donde el vector ω es el vector de velocidad angular obtenido de los componentes de la matriz [Ω]; el vector

es la posición de P con respecto al origen O del cuadro móvil M; y

Es la velocidad del origen O.

Aceleración
La aceleración de un punto P en un cuerpo móvil B se obtiene como la derivada temporal de su vector de velocidad: 

Esta ecuación se puede ampliar en primer lugar computando

y

La fórmula para la aceleración A _P ahora se puede obtener como:

o

donde α es el vector de aceleración angular obtenido de la derivada de la matriz de velocidad angular;

es el vector de posición relativa (la posición de P en relación con el origen O del marco móvil M); y

Es la aceleración del origen del cuadro móvil M.