Les lois de Grassmann en science des couleurs

Les lois de Grassmann décrivent des résultats empiriques sur la façon dont la perception des mélanges de lumières colorées (c.-à-d., Les lumières qui co-stimulent la même zone sur la rétine) composées de différentes distributions de puissance spectrale peuvent être reliées algébriquement les unes aux autres. Découvertes par Hermann Grassmann, ces « lois » sont en fait des principes utilisés pour prédire les réponses des couleurs à une bonne approximation sous vision photopique et mésopique. Un certain nombre d’études ont examiné comment et pourquoi ils fournissent de mauvaises prédictions dans des conditions spécifiques.
Interprétation moderne
Les quatre lois sont décrites dans des textes modernes avec des degrés divers de notation algébrique et sont résumées comme suit (les définitions précises des nombres et des corollaires peuvent varier d’une source à l’autre):
Première loi: Deux lumières colorées apparaissent différentes si elles diffèrent par la longueur d’onde dominante, la luminance ou la pureté. Corollaire: Pour chaque lumière colorée, il existe une lumière avec une couleur complémentaire telle qu’un mélange des deux lumières désature le composant le plus intense ou donne une lumière incolore (gris / blanc).
Chaque impression de couleur peut être complètement décrite avec exactement trois tailles de base.
Notation mathématique:
Graßmann lui-même aime utiliser les trois quantités de base de la couleur de base (couleur spectrale), l’intensité de la couleur et l’intensité du blanc. Aujourd’hui, cette trinité est appelée espace de couleur HSV et est modélisée comme un cône dans l’image adjacente; les abréviations représentent Hue (teinte), Saturation (saturation) et Value of Lightness (Également Brightness ou Luminance, darkness allemand). La loi est également applicable à trois couleurs primaires (telles que les valences primaires CIE ou RGB) – juste trois couleurs, dont chacune ne peut pas être faite par un mélange des deux autres.
Deuxième loi: L’apparition d’un mélange de lumière à partir de deux composants change si l’un ou l’autre des composants change. Corollaire: Un mélange de deux lumières colorées non complémentaires aboutit à un mélange dont la teinte varie en fonction de l’intensité relative de chaque lumière et de la saturation en fonction de la distance entre les teintes de chaque lumière.
La deuxième loi de Grassman sur la couleur additive mixture.png
Si l’on mélange une couleur avec une teinte changeante avec une couleur dans laquelle la teinte reste toujours la même, des couleurs avec une teinte changeante apparaissent, comme illustré par les intersections des surfaces de couleurs dans l’image d’accompagnement.
Notation mathématique:
Deux couleurs,
Ici, Graßmann décrit fondamentalement l’homogénéité (mathématique) de l’espace de couleur – peu importe quelle couleur change sur une couleur, le produit mélangé suit de manière analogue.
Troisième loi: Il y a des lumières avec différentes distributions de puissance spectrale mais elles semblent identiques. Premier corollaire: de telles lumières apparaissant identiques doivent avoir des effets identiques lorsqu’elles sont ajoutées à un mélange de lumière. Deuxième corollaire: de telles lumières apparaissant identiques doivent avoir des effets identiques lorsqu’elles sont soustraites (c’est-à-dire filtrées) d’un mélange de lumière.
La troisième loi de Grassman sur la couleur additive mixture.png
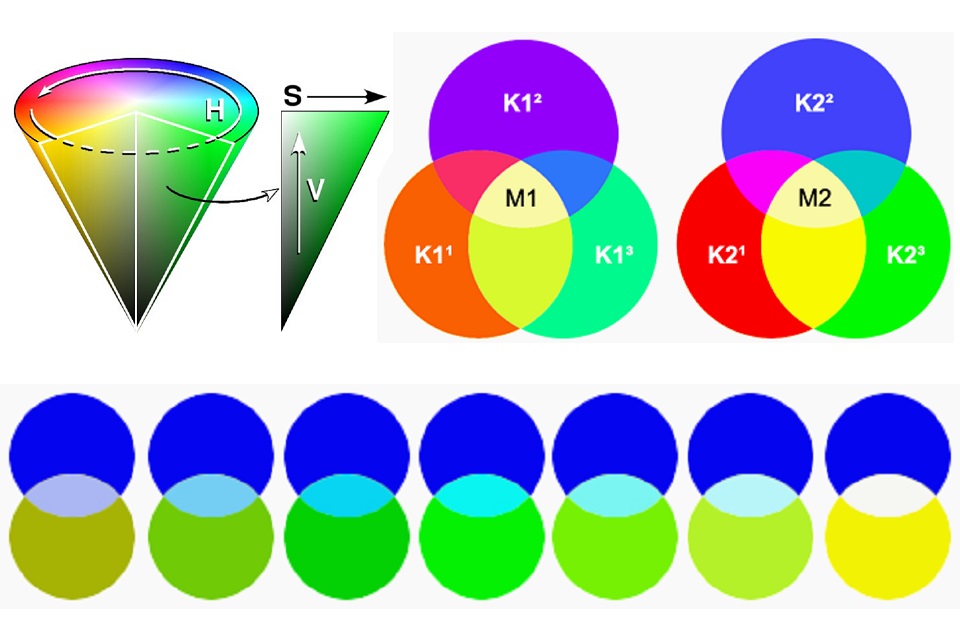
La teinte d’une couleur résultant du mélange de couleurs additives dépend uniquement de l’impression de couleur des couleurs de départ, mais pas de leurs compositions physiques (spectrales). L’image de droite montre la formation de deux couleurs métamères mutuellement plus (M1 et M2) à partir de différentes composantes de couleur (K1¹, K1² et K1³ ou K2¹, K2² et K2³).
Notation mathématique:
Cette loi stipule que le comportement de mélange des couleurs métamères même – c’est-à-dire celles avec la même impression de couleur mais en même temps une composition spectrale différente – peut être décrit exactement sur la base de leur impression de couleur. Inversement, aucune conclusion directe sur la composition spectrale d’une couleur ne peut être tirée du comportement de mélange.
Quatrième loi: L’intensité d’un mélange de lumières est la somme des intensités des composantes. Ceci est également connu comme la loi d’Abney.
La quatrième loi de Grassman sur la couleur additive mixture.png
L’intensité (ou l’intensité totale) d’une couleur mélangée additive (T3) correspond à la somme des intensités des couleurs de sortie
(dans le schéma limité à T1 et T2).
Notation mathématique:
Selon David L. MacAdam, cette loi ne s’applique qu’au cas particulier d’une source réduite idéalisée à un point, mais pas à des surfaces de couleur plus expansives. Graßmann n’avait traité que du cas spécial mentionné ci-dessus.
Ces lois impliquent une représentation algébrique de la lumière colorée. En supposant que les faisceaux 1 et 2 ont chacun une couleur, l’observateur choisit
La loi de Grassmann peut être exprimée sous une forme générale en indiquant que pour une couleur donnée avec une distribution spectrale de puissance {\ displaystyle I (\ lambda)} I (\ lambda), les coordonnées RGB sont données par:
Observez que ceux-ci sont linéaires dans
importance
Les postulats ne s’appliquent pas universellement à tous les êtres voyants, mais surtout au sens visuel humain. Les lois spécifient la signification générale de la trichromaticité. Ils permettent de faire des prédictions précises sur l’impression d’égalité des couleurs attendue et forment ainsi la base de la colorimétrie, à l’aide de laquelle, par exemple, la reproduction des couleurs imprimées ou la reproduction sur les moniteurs est standardisée. En général, cet enseignement des désignations de couleurs permet une description de la valence de couleur par des moyens graphiques, comme illustré sur l’image à droite d’un graphique de mélange de couleurs de Graßmann utilisant des vecteurs. Ce type de calcul est également fondamentalement basé sur le travail de Graßmann.
Première publication
Lorsque Hermann Ludwig Ferdinand von Helmholtz développa sa théorie tricolore vers 1850 sur la base d’une ancienne théorie de la perception des couleurs de Thomas Young, de nombreux scientifiques du XIXe siècle en ont fait état. Graßmann a basé ses considérations sur les théories de Sir Isaac Newton, qu’il avait développées dans son travail « Opticks: ou, un traité sur les réflexions, les réfractions, les inflexions et les couleurs de la lumière » (Londres 1704).
En traitant de quelques conclusions erronées de Helmholtz (1852), qui corrigeaient cela après l’apparition de l’œuvre de Graßmann, Graßmann a clarifié la théorie des couleurs de Newton et ceci précisément affiné en termes de description dans un espace de couleurs. En février 1853, il publia un article dans « Les Annales de Physique et de Chimie de Poggendorff »
Le livre intitulé « The Theory of Color Mixing » commence par les mots suivants:
« M. Helmholtz partage une série d’observations en partie nouvelles et ingénieuses, dont il conclut que la théorie du mélange des couleurs est généralement admise puisque Newton est erroné dans les points les plus essentiels, et qu’il n’y a que deux couleurs prismatiques, jaune et indigo, blanc. Par conséquent, il ne serait pas superflu de montrer comment la théorie de Newton du mélange des couleurs atteint un certain point, et surtout la proposition que chaque couleur a sa couleur complémentaire, qui lui mélange blanc, à partir de faits indéniables avec des preuves mathématiques. cette phrase doit être considérée comme l’une des plus fondées en physique. Je montrerai ensuite comment les observations positives faites par Helmholtz, au lieu de témoigner contre cette théorie, peuvent servir à le confirmer, en partie pour le compléter. »
Il donne ses « lois de la couleur mélangeant » le libellé suivant:
1. (…) « chaque impression de couleur [se décompose] (…) en trois moments mathématiquement déterminables (…): le ton de la couleur, l’intensité de la couleur et l’intensité du blanc mélangé. »
2. (…) « si l’une des deux lumières à mélanger change continuellement d’une chose (…), l’impression du mélange change aussi constamment. »
3. Il y a «(…) deux couleurs dont chacune a une teinte constante, une intensité de couleur constante et une intensité constante du blanc mélangé, ainsi qu’un mélange constant de couleurs (…), quelles que soient les couleurs homogènes ceux qui sont composés. »
4. (…) « l’intensité lumineuse totale du mélange la somme (…) des intensités des lumières mixtes. »
Cercle de couleur Grassman 1853.png
Par exemple, il a ajouté diverses représentations graphiques, comme le montre la figure ci-contre à titre d’exemple. En utilisant cette représentation géométrique des relations au niveau de la couleur, il décrit un mélange particulier de proportions de couleurs A et B en utilisant les définitions et les termes suivants:
A et B sont des couleurs homogènes, O est le point blanc;
D représente la saturation maximale et le point de couleur C correspond à la teinte dans sa gravité.
(a + b) OC signifie l’intensité des composantes de la couleur.
(a + b) CD représente l’intensité de la composante blanche.
(a + b) OD (avec DO = 1) exprime l’intensité totale.