Légèreté – HiSoUR Art Culture Histoire

In der Farbmetrik und Farbtheorie ist die Helligkeit, auch bekannt als Wert oder Ton, eine Darstellung der Variation in der Wahrnehmung der Helligkeit einer Farbe oder eines Farbraums. Es ist einer der Farberscheinungsparameter eines beliebigen Farbenerscheinungsmodells.

Verschiedene Farbmodelle haben einen expliziten Begriff für diese Eigenschaft. Das Munsell-Farbmodell verwendet den Begriff Wert, während das HSL-Farbmodell, der HCL-Farbraum und der Lab-Farbraum den Begriff Helligkeit verwenden. Das HSV-Modell verwendet den Begriff Wert ein wenig anders: Eine Farbe mit einem niedrigen Wert ist fast schwarz, aber eine mit einem hohen Wert ist die reine, voll gesättigte Farbe.

In subtraktiven Farben (z. B. Farben) können Wertänderungen durch Hinzufügen von Schwarz oder Weiß zur Farbe erreicht werden. Dies verringert jedoch auch die Sättigung. Chiaroscuro und Tenebris nutzen beide dramatische Gegensätze, um das Drama in der Kunst zu erhöhen. Künstler können auch Schattierungen, subtile Wertmanipulationen einsetzen.

Beziehung zu Wert und relativer Leuchtdichte
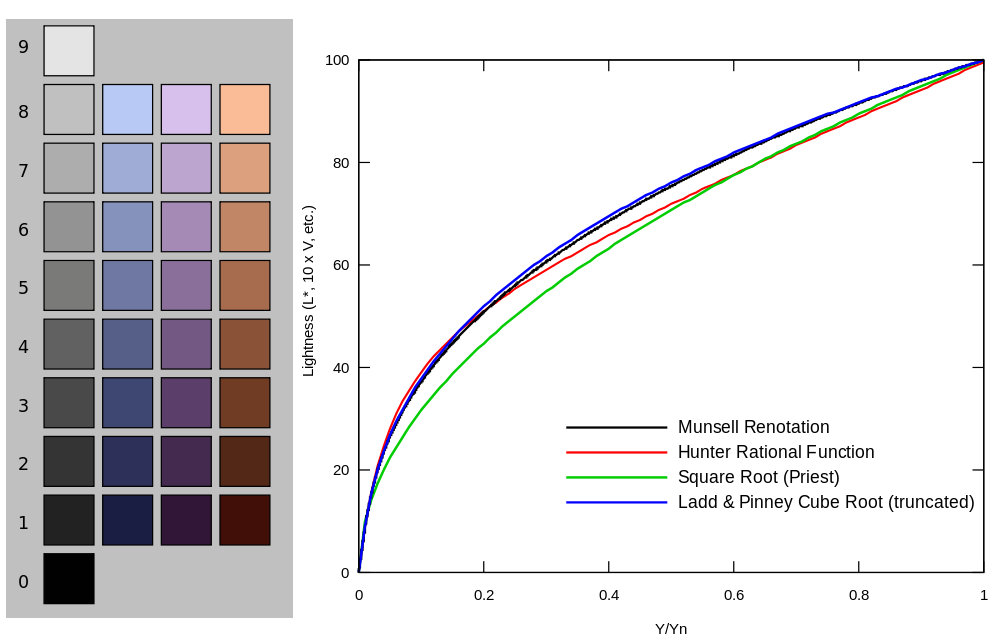
Der Munsell-Wert wurde lange als eine wahrnehmbar gleichförmige Helligkeitsskala verwendet. Eine Frage von Interesse ist die Beziehung zwischen der Munsell-Werteskala und der relativen Leuchtdichte. Im Bewusstsein des Weber-Fechner-Gesetzes bemerkte Munsell: « Sollen wir eine logarithmische Kurve oder eine quadratische Kurve verwenden? » Keine der beiden Optionen erwies sich als richtig. Die Wissenschaftler konvergierten schließlich auf einer ungefähren Kubikwurzelkurve, die mit dem Stevens’schen Potenzgesetz für die Helligkeitswahrnehmung übereinstimmt, was die Tatsache widerspiegelt, dass die Helligkeit proportional zur Anzahl der Nervenimpulse pro Nervenfaser pro Zeiteinheit ist. Der Rest dieses Abschnitts ist eine Chronologie der Helligkeitsnäherung, die zu CIE LAB führt.

Hinweis. – Munsell’s V läuft von 0 bis 10, während Y typischerweise von 0 bis 100 läuft (oft als Prozentsatz interpretiert). Typischerweise wird die relative Luminanz normalisiert, so dass das « Referenzweiß » (zum Beispiel Magnesiumoxid) einen Tristimulus-Wert von Y = 100 hat. Da das Reflexionsvermögen von Magnesiumoxid (MgO) relativ zu dem perfekt reflektierenden Diffusor 97,5% beträgt, ist V = 10 entspricht Y = 100 / 97,5% & ap; 102,6, wenn MgO als Referenz verwendet wird.

1920
Priester et al. eine Basisschätzung des Munsell-Wertes liefern (wobei Y in diesem Fall von 0 bis 1 läuft):
${\ displaystyle V = 10 {\ sqrt {Y}}.}$
1933
Munsell, Sloan und Godlove starten eine Studie über die Munsell-Neutralwertskala unter Berücksichtigung mehrerer Vorschläge, die die relative Leuchtdichte auf den Munsell-Wert beziehen, und schlagen vor:
${\ displaystyle V ^ {2} = 1.474,2Y-0.004.743Y ^ {2}.}$
1943
Newhall, Nickerson und Judd bereiten einen Bericht für die Optical Society of America vor. Sie schlagen eine quintische Parabel vor (die das Reflexionsvermögen in Bezug auf den Wert in Beziehung setzt):
${\ displaystyle Y = 1.221,9V-0.231,11V ^ {2} + 0,239,51V ^ {3} -0,021,009V ^ {4} + 0,000840,4V ^ {5}}$
1943
In Tabelle II des OSA-Berichts drücken Moon und Spencer den Wert der relativen Leuchtdichte aus:
${\ displaystyle V = 5 (Y / 19.77) ^ {0.426} = 1.4Y ^ {0.426}}$
1944
Saunderson und Milner führen im vorhergehenden Ausdruck eine subtraktive Konstante ein, um besser zum Munsell-Wert zu passen. Später behaupten Jameson und Hurvich, dass dies gleichzeitige Kontrasteffekte korrigiert.
${\ displaystyle V = 2.357Y ^ {0.343} -1.52.}$
1955
Ladd und Pinney von Eastman Kodak interessieren sich für den Munsell-Wert als wahrnehmbar einheitliche Helligkeitsskala für den Einsatz im Fernsehen.Nachdem sie eine logarithmische und fünf Potenzgesetzfunktionen betrachtet haben (nach Stevens Potenzgesetz), beziehen sie den Wert auf das Reflexionsvermögen, indem sie das Reflexionsvermögen auf die Potenz von 0.352 erhöhen:
${\ displaystyle V = 2.217Y ^ {0.352} -1.324.}$
Dies zu erkennen ist ziemlich nah an der Kubikwurzel, sie vereinfachen es zu:
${\ displaystyle V = 2,468Y ^ {1/3} -1,636.}$
1958
Glasser et al. Definieren Sie die Helligkeit als zehn Mal den Munsell-Wert (so dass die Helligkeit von 0 bis 100 reicht):
${\ displaystyle L ^ {\ stern} = 25.29Y ^ {1/3} -18.38.}$
1964
Wyszecki vereinfacht dies zu:
${\ displaystyle W ^ {\ stern} = 25Y ^ {1/3} -17.}$
Diese Formel approximiert die Munsell-Wertfunktion für 1% < Y <98% (gilt nicht für Y <1% ) und wird für den CIE 1964-Farbraum verwendet.

1976

CIE LAB verwendet die folgende Formel:

${\ displaystyle L ^ {\ stern} = 116 (Y / Y _ {\ mathrm {n}}) ^ {1/3} -16.}$

wobei Yn der CIE XYZ Y-Normfarbwert des Referenzweißpunkts ist (der Index n schlägt « normalisiert » vor) und unterliegt der Einschränkung Y / Yn> 0,01. Pauli beseitigt diese Einschränkung, indem er eine lineare Extrapolation berechnet, die Y / Yn = 0 auf L * = 0 abbildet und tangential zur obigen Formel an dem Punkt ist, an dem die lineare Erweiterung wirksam wird. Zuerst wird der Übergangspunkt als Y / Yn = (6/29) ^ 3 ≈ 0,008,856 bestimmt, dann wird die Steigung von (29/3) ^ 3 ≈ 903,3 berechnet. Dies ergibt die zweiteilige Funktion:
${\ displaystyle f (t) = {\ begin {Fälle} t ^ {1/3} & {\ Text {if}} t> {\ big (} {\ frac {6} {29}} {\ big) } ^ {3} \\ {\ frac {1} {3}} {\ gross (} {\ frac {29} {6}} {\ gross}} ^ {2} t + {\ frac {4} {29 }} & {\ text {sonst}} \ end {cases}}}$
Die Leichtigkeit ist dann:
${\ displaystyle L ^ {\ stern} = 116f (Y / Y _ {\ mathrm {n}}) - 16.}$
Auf den ersten Blick könnte man die Helligkeitsfunktion durch eine Kubikwurzel approximieren, eine Approximation, die man in der Fachliteratur findet. Das lineare Segment in der Nähe von Schwarz ist jedoch signifikant, und so die Koeffizienten 116 und 16. Die am besten geeignete reine Potenzfunktion hat einen Exponenten von etwa 0,42, weit entfernt von 1/3.

Eine ungefähr 18% graue Karte, mit einem exakten Reflexionsvermögen von $\ links (33/58 \ rechts) ^ 3$ , hat einen Helligkeitswert von 50. Es wird « mittelgrau » genannt, weil seine Helligkeit in der Mitte zwischen Schwarz und Weiß liegt.

Andere psychologische Auswirkungen
Diese subjektive Wahrnehmung von Luminanz in nicht-linearer Weise ist eine Sache, die die Gammakompression von Bildern lohnend macht. Neben diesem Phänomen gibt es noch andere Effekte, die die Wahrnehmung von Leichtigkeit betreffen. Chromacity kann die wahrgenommene Helligkeit beeinflussen, wie sie durch den Helmholtz-Kohlrausch-Effekt beschrieben wird. Obwohl der CIE LAB-Raum und Verwandte diesen Effekt auf die Helligkeit nicht berücksichtigen, kann er im Munsell-Farbmodell enthalten sein. Wie beim Purkinje-Effekt können auch Lichtniveaus die wahrgenommene Farbigkeit beeinflussen.