La syntaxe

Le terme syntaxe spatiale englobe un ensemble de théories et de techniques pour l’analyse des configurations spatiales. Il a été conçu par Bill Hillier, Julienne Hanson et ses collègues à The Bartlett, University College London à la fin des années 1970 jusqu’au début des années 1980 comme un outil pour aider les urbanistes à simuler les effets sociaux probables de leurs conceptions.

Thèse
L’idée générale est que les espaces peuvent être décomposés en composants, analysés comme des réseaux de choix, puis représentés sous forme de cartes et de graphiques décrivant la connectivité relative et l’intégration de ces espaces. Il repose sur trois conceptions de base de l’espace:

un isoviste (popularisé par Michael Benedikt à l’Université du Texas), ou viewshed ou polygone de visibilité, le champ de vision à partir d’un point particulier
espace axial (idée popularisée par Bill Hillier à l’UCL), une ligne de vue droite et un chemin possible
espace convexe (popularisé par John Peponis et ses collaborateurs chez Georgia Tech), un vide occupable où, si l’on imagine un diagramme filaire, aucune ligne entre deux de ses points ne sort de son périmètre: tous les points du polygone sont visibles par tous les autres points dans le polygone.
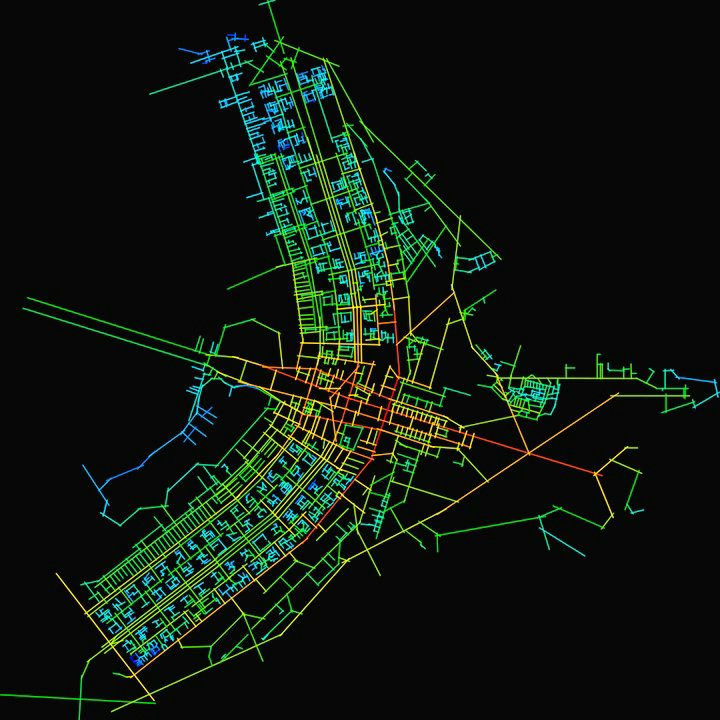
Les trois façons les plus populaires d’analyser un réseau routier sont l’intégration, le choix et la distance de profondeur.

L’intégration mesure le nombre de virages à effectuer à partir d’un segment de rue pour atteindre tous les autres segments de rue du réseau, en utilisant les chemins les plus courts. Si l’on analyse le nombre de tours requis pour atteindre tous les segments du graphique, on dit que l’analyse mesure l’intégration au rayon ‘n’. Le premier segment d’intersection ne nécessite qu’un seul tour, les deux autres tours et ainsi de suite. Les segments de rue qui nécessitent le moins de virages pour atteindre toutes les autres rues sont appelés «les plus intégrés» et sont généralement représentés avec des couleurs plus chaudes, comme le rouge ou le jaune. L’intégration peut également être analysée à l’échelle locale au lieu de l’échelle de l’ensemble du réseau. Dans le cas du rayon 4, par exemple, seulement quatre tours sont comptés au départ de chaque segment de rue.
Théoriquement, la mesure d’intégration montre la complexité cognitive de l’atteinte d’une rue, et est souvent considérée comme «prédictive» de l’usage d’une rue par les piétons: plus il est facile d’atteindre une rue, plus elle devrait être populaire. Bien qu’il y ait des preuves que cela soit vrai, la méthode est orientée vers de longues rues droites qui se croisent avec beaucoup d’autres rues. Ces rues, comme Oxford Street à Londres, ressortent comme particulièrement fortement intégrées. Cependant, une rue légèrement sinueuse de la même longueur serait typiquement segmentée en segments droits individuels, non comptés comme une seule ligne, ce qui rendrait les rues sinueuses moins intégrées dans l’analyse.

La mesure du choix est plus facile à comprendre en tant que «débit d’eau» dans le réseau routier. Imaginez que chaque segment de rue reçoive une charge initiale d’une unité d’eau, qui commence alors à dériver du segment de rue de départ vers tous les segments qui s’y connectent successivement. Chaque fois qu’une intersection apparaît, la valeur restante du débit est divisée également entre les rues de division, jusqu’à ce que tous les autres segments de rue dans le graphique soient atteints. Par exemple, à la première intersection avec une seule autre rue, la valeur initiale de l’une est divisée en deux valeurs restantes d’une moitié et allouées aux deux segments de rue qui se croisent. En descendant plus bas, la moitié restante est à nouveau divisée entre les rues qui s’entrecroisent et ainsi de suite. Lorsque la même procédure a été effectuée en utilisant chaque segment comme point de départ pour la valeur initiale de un, un graphique des valeurs finales apparaît. Les rues ayant les valeurs totales les plus élevées du débit accumulé sont considérées comme ayant les valeurs de choix les plus élevées.
Comme l’intégration, l’analyse de Choice peut être limitée à des rayons locaux limités, par exemple 400m, 800m, 1600m. Interpréter l’analyse des choix est plus délicat que l’intégration. La syntaxe de l’espace fait valoir que ces valeurs prédisent souvent le flux de circulation automobile des rues, mais, à proprement parler, l’analyse de Choix peut également être considérée comme représentant le nombre d’intersections qui doivent être franchies pour atteindre une rue. Cependant, puisque les valeurs de flux sont divisées (non soustraites) à chaque intersection, la sortie montre une distribution exponentielle. Il est préférable de prendre un journal de la base deux des valeurs finales afin d’obtenir une image plus précise.

La distance de profondeur est la plus intuitive des méthodes d’analyse. Il explique la distance linéaire entre le point central de chaque segment de rue et les points centraux de tous les autres segments. Si chaque segment est successivement choisi comme point de départ, un graphique des valeurs finales cumulatives est obtenu. Les rues ayant les valeurs de distance de profondeur les plus basses seraient les plus proches de toutes les autres rues. Encore une fois, le rayon de recherche peut être limité à n’importe quelle distance.
Applications
A partir de ces composants, il est possible de quantifier et de décrire la facilité de navigation de tout espace utile pour la conception de musées, d’aéroports, d’hôpitaux et d’autres lieux où l’orientation est un problème important. La syntaxe spatiale a également été appliquée pour prédire la corrélation entre les dispositions spatiales et les effets sociaux tels que la criminalité, le flux de trafic et les ventes par unité de surface.

Histoire
La syntaxe spatiale s’est développée pour devenir un outil utilisé dans le monde entier dans divers domaines de recherche et applications de conception en architecture, design urbain, planification, transport et design d’intérieur. En général, l’analyse utilise l’un des nombreux logiciels qui permettent aux chercheurs d’analyser les graphiques d’un (ou de plusieurs) des composants spatiaux primaires.

Au cours de la dernière décennie, les techniques de syntaxe spatiale ont été utilisées pour la recherche en archéologie, en technologie de l’information, en géographie urbaine et humaine et en anthropologie. Depuis 1997, la communauté de la syntaxe spatiale a tenu des conférences biennales et de nombreux articles de revues ont été publiés sur le sujet, principalement dans le domaine de l’environnement et de la planification B.

Critique
La fiabilité mathématique de la syntaxe spatiale a récemment fait l’objet d’un examen en raison d’un certain nombre de paradoxes qui se posent dans certaines configurations géométriques. Ces paradoxes ont été soulignés par Carlo Ratti au Massachusetts Institute of Technology, mais niés dans un échange universitaire passionné avec Bill Hillier et Alan Penn [2004]. Il y a eu des tentatives de retour pour combiner la syntaxe spatiale avec des modèles d’ingénierie de transport plus traditionnels, en utilisant des intersections comme nœuds et en construisant des graphiques de visibilité pour les relier, par des chercheurs comme Bin Jiang, Valerio Cutini et Michael Batty. Récemment, des travaux de recherche ont également été menés en combinant la syntaxe spatiale avec l’analyse de l’accessibilité géographique dans les SIG, tels que les modèles de syntaxe spatiale mis au point par le groupe de recherche Spatial Analysis and Design du Royal Institute of Technology de Stockholm. Une série de http://journals.sagepub.com/doi/abs/10.1068/b32045 travaux interdisciplinaires publiés à partir de 2006 par Vito Latora, Sergio Porta et ses collègues, proposant une approche en réseau pour l’analyse et la conception de la centralité des rues, ont mis en évidence la syntaxe spatiale ‘ contribution à des décennies d’études antérieures en physique des réseaux spatiaux complexes.