Réseau spatial

Un réseau spatial (parfois aussi un graphique géométrique) est un graphe dans lequel les sommets ou arêtes sont des éléments spatiaux associés à des objets géométriques, c’est-à-dire que les nœuds sont situés dans un espace équipé d’une certaine métrique. La réalisation mathématique la plus simple est un treillis ou un graphe géométrique aléatoire, où les nœuds sont répartis uniformément au hasard sur un plan bidimensionnel; une paire de nœuds est connectée si la distance euclidienne est inférieure à un rayon de voisinage donné. Les réseaux de transport et de mobilité, Internet, les réseaux de téléphonie mobile, les réseaux électriques, les réseaux sociaux et de contact et les réseaux de neurones sont des exemples où l’espace sous-jacent est pertinent et où la topologie du graphique ne contient pas toute l’information. Caractériser et comprendre la structure, la résilience et l’évolution des réseaux spatiaux est crucial pour de nombreux domaines allant de l’urbanisme à l’épidémiologie.

Exemples
Un réseau spatial urbain peut être construit en faisant abstraction des intersections comme des nœuds et des rues en tant que liens, ce qui est appelé réseau de transport. Le trafic de Beijing a été étudié en tant que réseau dynamique et ses propriétés de percolation ont été jugées utiles pour identifier les goulots d’étranglement systématiques.

On pourrait penser à la «carte de l’espace» comme étant l’image négative de la carte standard, avec l’espace ouvert coupé des bâtiments de fond ou des murs.

Caractériser les réseaux spatiaux
Les aspects suivants sont quelques-unes des caractéristiques pour examiner un réseau spatial:

Réseaux planaires
Dans de nombreuses applications, telles que le rail, les routes et d’autres réseaux de transport, le réseau est supposé être planaire. Les réseaux planaires construisent un groupe important hors des réseaux spatiaux, mais tous les réseaux spatiaux ne sont pas planaires. En effet, les réseaux de passagers aériens sont un exemple non planaire: tous les aéroports du monde sont reliés par des vols directs.

La façon dont il est intégré dans l’espace
Il existe des exemples de réseaux qui ne semblent pas être «directement» intégrés dans l’espace. Les réseaux sociaux, par exemple, connectent les individus à travers des relations d’amitié. Mais dans ce cas, l’espace intervient dans le fait que la probabilité de connexion entre deux individus diminue habituellement avec la distance qui les sépare.

Vessonoi tessellation
Un réseau spatial peut être représenté par un diagramme de Voronoï, qui est un moyen de diviser l’espace en un certain nombre de régions. Le graphique double pour un diagramme de Voronoï correspond à la triangulation de Delaunay pour le même ensemble de points. Les tessellations de Voronoi sont intéressantes pour les réseaux spatiaux en ce sens qu’elles fournissent un modèle de représentation naturel auquel on peut comparer un réseau du monde réel.

Mélange d’espace et de topologie
L’examen de la topologie des nœuds et des arêtes est une autre façon de caractériser les réseaux. La distribution du degré des nœuds est souvent considérée, en ce qui concerne la structure des arêtes, il est utile de trouver l’arbre couvrant minimum, ou la généralisation, l’arbre de Steiner et le graphique de voisinage relatif

Réseaux de treillis
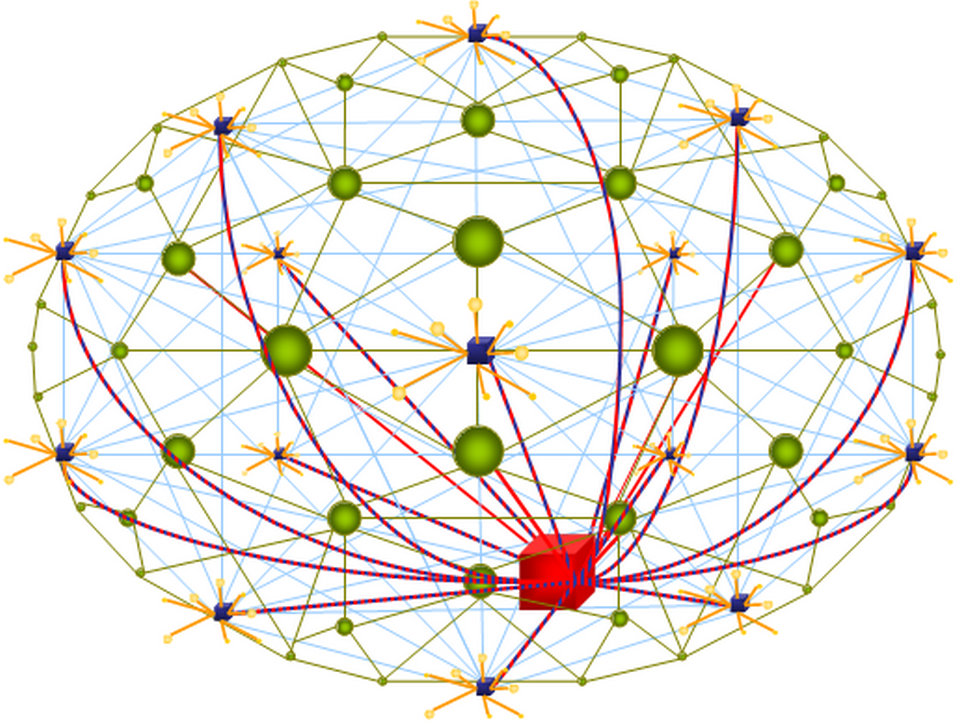
Les réseaux en treillis (voir Fig. 1) sont des modèles utiles pour les réseaux spatiaux intégrés. De nombreux phénomènes physiques ont été étudiés sur ces structures. Les exemples incluent le modèle d’Ising pour l’aimantation spontanée, les phénomènes de diffusion modélisés comme des marches aléatoires et la percolation. Récemment, pour modéliser la résilience d’infrastructures interdépendantes spatialement intégrées, un modèle de réseaux réticulaires interdépendants a été introduit (voir Fig. 2) et analysé. Un modèle multiplex spatial a été introduit par Danziger et al et a été analysé par Vaknin et al.

Probabilité et réseaux spatiaux
Dans le monde «réel», de nombreux aspects des réseaux ne sont pas déterministes – le hasard joue un rôle important. Par exemple, de nouveaux liens, représentant des amitiés, dans les réseaux sociaux sont d’une certaine manière aléatoire. La modélisation des réseaux spatiaux à l’égard des opérations stochastiques est conséquente. Dans de nombreux cas, le processus de Poisson spatial est utilisé pour approximer des ensembles de données de processus sur des réseaux spatiaux. D’autres aspects stochastiques d’intérêt sont:

Le processus de la ligne de Poisson
Géométrie stochastique: le graphique d’Erdős-Rényi
Théorie de la percolation
Approche de la théorie de la syntaxe spatiale
Une autre définition du réseau spatial dérive de la théorie de la syntaxe spatiale. Il peut être notoirement difficile de décider quel élément spatial devrait être dans des espaces complexes impliquant de grandes zones ouvertes ou de nombreux chemins interconnectés. Les initiateurs de la syntaxe spatiale, Bill Hillier et Julienne Hanson utilisent des lignes axiales et des espaces convexes comme éléments spatiaux. Autrement dit, une ligne axiale est la «ligne de visée et d’accès la plus longue» à travers un espace ouvert, et un espace convexe est le «polygone convexe maximal» qui peut être dessiné dans un espace ouvert. Chacun de ces éléments est défini par la géométrie de la limite locale dans différentes régions de la carte spatiale. La décomposition d’une carte d’espace en un ensemble complet de lignes axiales entrecroisées ou d’espaces convexes se chevauchant produit respectivement la carte axiale ou la carte convexe qui se chevauche. Des définitions algorithmiques de ces cartes existent, ce qui permet de mapper à partir d’une carte spatiale de forme arbitraire vers un réseau susceptible de représenter graphiquement des mathématiques à effectuer d’une manière relativement bien définie. Les cartes axiales sont utilisées pour analyser les réseaux urbains, où le système comprend généralement des segments linéaires, tandis que les cartes convexes sont plus souvent utilisées pour analyser les plans de construction où les motifs spatiaux sont souvent plus convexes.

Actuellement, il y a un mouvement au sein de la communauté de la syntaxe spatiale pour mieux s’intégrer aux systèmes d’information géographique (SIG), et la plupart des logiciels qu’ils produisent interagissent avec les systèmes SIG disponibles dans le commerce.

Histoire
Alors que les réseaux et les graphiques faisaient déjà depuis longtemps l’objet de nombreuses études en mathématiques, en sociologie mathématique, en informatique, les réseaux spatiaux ont été étudiés intensivement dans les années 1970 en géographie quantitative. Les objets d’études en géographie sont entre autres les lieux, les activités et les flux d’individus, mais aussi les réseaux évoluant dans le temps et l’espace. La plupart des problèmes importants tels que la localisation des nœuds d’un réseau, l’évolution des réseaux de transport et leur interaction avec la population et la densité d’activité sont abordés dans ces études antérieures. D’un autre côté, de nombreux points importants restent encore flous, en partie parce qu’à cette époque, les ensembles de données de grands réseaux et de capacités informatiques plus importantes manquaient. Récemment, les réseaux spatiaux ont fait l’objet d’études en statistique, pour relier les probabilités et les processus stochastiques aux réseaux dans le monde réel.