
多接合太陽電池は、異なる半導体材料の複数のp-n接合を有する太陽電池である。 各材料の各pn接合は、異なる波長の光に応答して電流を生成する。 単純なセルは、太陽光のスペクトル内の単一波長の電流を生成する。 多接合セル太陽電池は、光の複数の波長で電流を生成し、使用可能な電気エネルギーに対する太陽光のエネルギー変換効率を高める。
伝統的な単一組合細胞は、最大理論効率が33.16%である。 理論的には、非常に集中した太陽光の下で無限の数の接合部が86.8%の限界効率を有する。
現在、伝統的な結晶シリコン太陽電池の最良の実験室の例は、20%〜25%の効率を有するが、多重接合セルの実験例は、濃縮太陽光下で46%を超える歩留まりを示している。 タンデム細胞の商業的な例は、1つの太陽光で30%、太陽光で約40%に改善されている。 しかし、この効率は、より複雑さと製造コストを犠牲にして得られる。 今日まで、その高い価格とより高い価格/性能比は、特に高い出力/重量比が望ましい航空宇宙分野における特殊機能への使用を制限していた。 地上のアプリケーションでは、これらの太陽電池は光起電性集光器(CPV)に出現しており、世界中の設備が増えています。
タンデム製造技術は、既存の設計の性能を改善するために使用されてきた。 特に、この技術は、従来の結晶シリコンと異なり、軽量で可撓性の約10%の効率を有するセルを製造するために、アモルファスシリコンを使用する低コストの薄膜太陽電池に適用することができる。 このアプローチは、いくつかの商業的供給業者によって使用されてきたが、これらの製品は現在屋根材など特定のニッチな役割に限定されている。
伝統的なシングルユニオンセルは最大理論効率が34%です。 理論的に無限の数の接合部では、多接合セルの効率は、高度に集中した太陽光のもとで87%になる。
現在、伝統的なシリコン太陽電池の最良の実験室の例は約25%の効率を有し、多接合セルの実験例は43%を超える性能を示している。
説明
多接合セル
複数の材料層から作製されたセルは、複数のバンドギャップを有することができ、したがって、上述のように緩和に失われるエネルギーの一部を捕捉して変換する、複数の光波長に応答する。
例えば、一方が赤色光に、もう一方が緑色に調整された2つのバンドギャップを有するセルを有する場合、緑色、シアンおよび青色光の余分なエネルギーは、緑色感光性材料のバンドギャップにのみ失われ、赤色、黄色およびオレンジ色のエネルギーは、赤色感光性材料のバンドギャップにのみ失われる。 シングルバンドギャップデバイスで行われたものと同様の分析に続いて、2ギャップデバイスの完全なバンドギャップが1.1eVおよび1.8eVであることを実証することができる。
都合のよいことに、特定の波長の光は、より大きなバンドギャップの材料と強く相互作用しない。これは、異なる材料を重ね合わせることによってマルチジャンクションセルを作ることができることを意味します。最上部の最短波長(最大バンドギャップ)とセルのボディを通って増加します。吸収されるべき適切な層に到達するために光子がセルを通過しなければならないので、各層で生成される電子を収集するために透明な導体を使用する必要がある。
タンデムセルを製造することは、材料の薄さおよび層の間の電流の抽出が困難であることが主な理由で、容易な作業ではない。 簡単な解決法は、2つの機械的に分離した薄膜太陽電池を使用し、次いでそれらをセルの外側で別々に配線することである。 この技術はアモルファスシリコン太陽電池で広く使用されており、Uni-Solar社の製品は3つの層を使用して約9%の効率を達成しています。 よりエキゾチックな薄膜材料を使用した実験室の例は、30%以上の効率を示しています。
より困難な解決法は、セルが機械的および電気的に接続された多数の層からなる「モノリシックに集積された」セルである。 これらのセルは、各層の電気的特性を慎重に一致させる必要があるため、製造するのがずっと困難です。 特に、各層に発生する光電流を一致させる必要があり、そうでなければ電子は層の間に吸収される。 これは、III-V半導体が最もよく満たす特定の材料にその構造を限定する。
材料選択
各サブセルの材料の選択は、格子整合、電流整合、および高性能光電子特性の要件によって決定される。
最適な成長および結果としての結晶品質のためには 、各材料の結晶格子定数aを厳密に一致させなければならず、格子整合デバイスが得られる。 この制約は、小さな程度の格子不整合を含む最近開発された変成太陽電池では幾分緩和されている。 しかしながら、より大きな程度のミスマッチまたは他の成長不完全性は、電子特性の劣化を引き起こす結晶欠陥をもたらし得る。
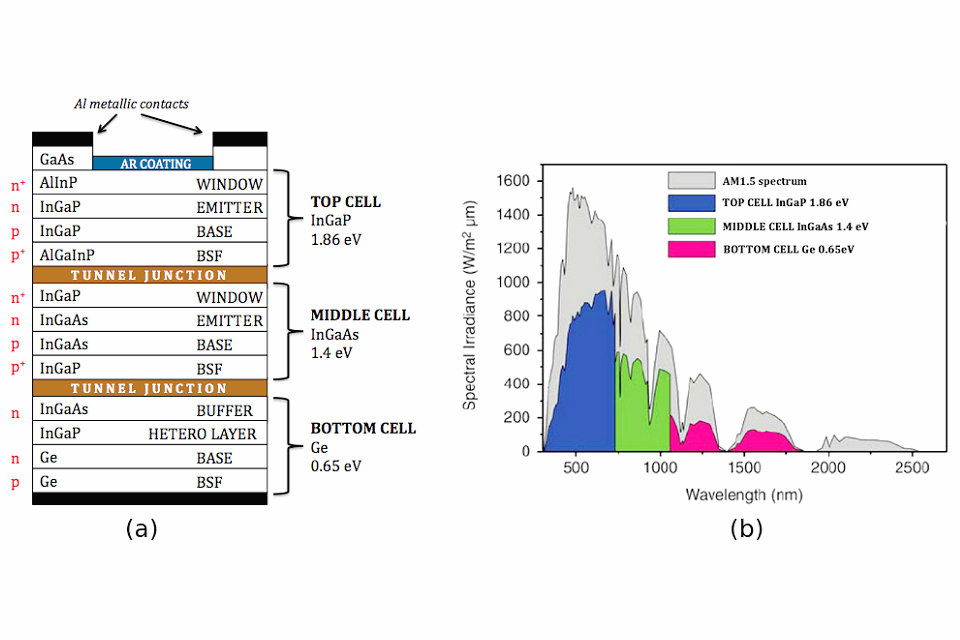
各サブセルは電気的に直列に接続されているので、各接合部には同じ電流が流れる。 材料は、サブバンドギャップ光( hc /λ<e・E g )が下方のサブセルに透過することを可能にする、減少するバンドギャップE gを有するように順序付けられる。 したがって、適切なバンドギャップは、設計スペクトルが各サブセルの現在の世代のバランスをとり、電流マッチングを達成するように選択されなければならない。 図C(b)は、与えられた波長λにおける光源パワー密度であるスペクトル放射照度E (λ)をプロットしている。 それは、光電流への変換に利用可能な光子の数に直接関係する波長の関数として、各接合部の最大変換効率と共にプロットされている。
最後に、層は高性能のために電気的に最適でなければならない。 これは、強い吸収係数α(λ)、高い少数キャリア寿命τの少数 、および高い移動度μを有する材料の使用を必要とする。
以下の表の好ましい値は、多接合太陽電池に典型的に使用される材料の選択を正当化する:上部サブセル用のInGaP(E g = 1.8〜1.9eV)、中間サブセル用のInGaAs(E g = 1.4 eV)、および底部サブセル用のゲルマニウム(E g = 0.67eV)。 Geの使用は、格子定数、堅牢性、低コスト、豊富さ、および製造の容易さに主に起因する。
異なる層が密接に格子整合しているので、デバイスの製造は、典型的には、有機金属化学気相堆積(MOCVD)を用いる。 この技術は、分子線エピタキシー(MBE)よりも結晶品質が高く、大量生産が可能であるため好ましい方法です。
| 材料 | E g 、eV | a 、nm | 吸収 (λ=0.8μm)、1 /μm | μn、cm 2 /(V・s) | τp、μs | 硬度 (モース) | α、μm/ K | S 、m / s |
|---|---|---|---|---|---|---|---|---|
| c-Si | 1.12 | 0.5431 | 0.102 | 1400 | 1 | 7 | 2.6 | 0.1-60 |
| InGaP | 1.86 | 0.5451 | 2 | 500 | – | 5 | 5.3 | 50 |
| GaAs | 1.4 | 0.5653 | 0.9 | 8500 | 3 | 4-5 | 6 | 50 |
| Ge | 0.65 | 0.5657 | 3 | 3900 | 1000 | 6 | 7 | 1000 |
| InGaAs | 1.2 | 0.5868 | 30 | 1200 | – | – | 5.66 | 100-1000 |
構造要素
メタリックコンタクト
金属接点は、半導体層と接触する低抵抗電極である。 彼らはしばしばアルミニウムです。 これは、太陽電池アレイの負荷または他の部分への電気的接続を提供する。 彼らは通常、細胞の2つの側面にあります。 そして、照明面のシャドーイングが低減されるように、背面にあることが重要です。
無反射コーティング
反射防止(AR)コーティングは、一般に、MJ太陽電池の場合にはいくつかの層からなる。 最上部のAR層は、透過係数Tを増加させるために(通常ピラミッドのために光子がMJ構造を取り出すことができないため)、ピラミッドを有するNaOH表面テクスチャリングを通常有しているので、経路長材料中の光子の Rは1%に減少する。 2つのAR層L 1 (最上層、通常はSiO
2 )およびL 2 (通常TiO
2 )、そこになければならない
トンネル接合部
トンネル接合の主な目的は、低い電気抵抗と2つのサブセル間の光学的に低損失の接続を提供することです。
したがって、電子は空乏領域を容易に通過することができる。 トンネル接合のJ-V特性は、トンネル接合を用いて2つのp-n接合間に低い電気抵抗接続を有する理由を説明するので、非常に重要である。 図Dは、トンネル領域、負の微分抵抗領域および熱拡散領域の3つの異なる領域を示す。 電子が障壁をトンネリングすることができる領域をトンネリング領域と呼ぶ。 そこでは、電圧は、トンネリングしているいくつかの電子のエネルギーが障壁の反対側で利用可能なエネルギー状態に等しくなるように十分に低くなければならない。 その結果、トンネル接合を通る電流密度は高くなる(最大値は
MJ太陽電池性能の低下を避けるために、トンネル接合は、次の光電池、中間セル、すなわちEgTunnel > E gMiddleCellによって吸収される波長に対して透明でなければならない。
ウィンドウレイヤーと裏面フィールド
窓層は、表面再結合速度Sを減少させるために使用される。 同様に、背面電界(BSF)層は、トンネル接合に向かってキャリアの散乱を低減する。 これらの2つの層の構造は同じであり、電子(正孔)を捕獲するヘテロ接合である。 実際、電界E dにもかかわらず、これらは、図Eに示すように、十分なエネルギーを有さないため、ヘテロ接合によって形成される障壁の上に飛び越えることができない。したがって、電子(正孔)は正孔(電子)と再結合できず、障壁を通って ところで、ウィンドウとBSFレイヤは、次のpn接合で吸収される波長、すなわち、E gW indow > E gEmitterおよびEgBSF > E gEmitterに対して透明でなければならない。 さらに、格子定数はInGaPのものに近くなければならず、層は高度にドープされなければならない( n ≧10 18 cm -3 )。
JV特性
効率を最大にするためには、各サブセルはその最適なJVパラメータで動作する必要があり、各サブセルについて必ずしも等しいとは限らない。 それらが異なる場合、太陽電池を通る総電流は、3つのうちの最小のものである。 近似すると、MJ太陽電池の短絡電流と同じ関係になります。J SC = min(J SC1 、J SC2 、J SC3 )ここで、 J SCi (λ)は、サブセルiに対して所与の波長λを有する。
全J- V特性から直接J SC1 、J SC2 、J SC3を得ることができないため、量子効率QE (λ)が利用される。 これは、生成された電子 – 正孔対の量と、所与の波長λにおける入射光子との間の比を測定する。 サブセルiにおける対応する入射光の光束をφi(λ)とし、サブセルiの量子効率をQ E i (λ)とする。 定義上、これは以下のことに等しい:
の価値
同様に、
{\ displaystyle V_ {OCi}}の値は、
理論的な限界効率
私たちは、CH Henryによって考案されたグラフィカル量子効率(QE)解析を用いて理想的な無限多接合太陽電池の限界効率を推定することができます。 ヘンリーの方法を十分に利用するには、AM1.5分光放射照度の単位を光子束(すなわち光子数/ m 2 / s)の単位に変換する必要があります。そのためには、光子エネルギー当たりの単位面積あたりに入射する電磁放射線のパワーから光子エネルギー当たりの光子フラックス(すなわち、[W / m 2 / eV]から[光子/ m 2 / s / eV])。 この中間単位変換では、以下の点を考慮する必要があります。光子は、以下のように定義される明確なエネルギーを持っています。
(1):E ph = h・f = h・(c /λ)
ここでE phは光子エネルギー、hはプランク定数(h = 6.626×10 -34 [J・s])、cは光速(c = 2.998×10 8 [m / s])、fは周波数[1 / s]であり、λは波長である。
次に、ある放射照度E [W / m 2 / eV]に対する光子エネルギー当たりの光子束dn ph /dhνは、以下のように計算することができる。
(2):
この中間単位変換の結果として、AM1.5スペクトル放射照度は、光子エネルギー当たりの光子束の単位[[光子数/ m 2 / s / eV]
中間ユニット変換からの上記の結果に基づいて、光子エネルギーに対する光子エネルギー毎の光子束を数値積分することによって、光子流束を導出することができる。 数値的に積分された光子束は、以下のように台形則を用いて計算される。
(3):
この数値積分の結果として、AM1.5スペクトル放射照度は、光子束の単位[光子数/ m 2 / s]で与えられる。
hν<0.31eVの標準(AM1.5)太陽エネルギースペクトルは利用できないので、0eVから0.3096eVの小さな光子エネルギー範囲で光子束データは存在しないことに留意すべきである。 しかし、このデータが利用できない場合でも、半導体がバンドギャップエネルギーよりも大きい光子エネルギーに対して不透明であり、バンドギャップエネルギーよりも小さい光子エネルギーに対して透過性であるという妥当な仮定を用いて、唯一の利用可能なデータを用いて、 この仮定は、太陽電池の効率の最初の固有の損失を説明している。これは、単一接合太陽電池が広い太陽エネルギースペクトルに適切にマッチすることができないことに起因する。 しかしながら、現在のグラフQE分析は、依然として、太陽電池、放射性再結合の効率における第2の固有の損失を反映することができない。 放射性再結合を考慮するためには、最初に放射電流密度J radを評価する必要があります。 Shockley and Queisser法によれば、J radは以下のように近似することができる。
(4):
(5):
ここで、E gは電子ボルトであり、nは3.6であると評価され、GaAsの値である。 入射吸収熱放射J thは、J rad = V = 0で与えられる。
(6):
負荷に供給される電流密度は、吸収された太陽放射および熱放射に起因する電流密度の差、および上面から放出されるかまたは基板内に吸収される放射の電流密度である。 J ph = en phを定義すると、
(7):J = J ph + J th – J rad
第2項J thは 、E gを有するすべての半導体についてJ phと比較して無視できる。 上記のJ 番目の式の評価によって示されるように、≧0.3eVである。 したがって、以下の説明を簡略化するために、この用語を無視します。 次に、Jを次のように表現することができます。
(8):
開回路電圧は、J = 0に設定することによって求められる。
(9):
最大電力点(J m 、V m )は、導関数を測ることによって求められる
(10):
(11):
最後に、吸収された光子あたりの最大仕事量(W m )、Wmは
(12):
最後の3つの方程式を組み合わせると、
(13):
上記式を用いて、E g (またはn ph )の異なる値に対してW m (赤線)をプロットする。
現在、太陽電池の効率の2つの大きな内在的な損失を考慮して、HenryのグラフィカルQE解析を完全に使用することができます。 2つの主な固有の損失は、放射再結合と、単一接合太陽電池が広範な太陽エネルギースペクトルに適切に適合できないことである。 赤い線の陰になっている部分は、理想的な無限多接合太陽電池によって行われる最大の仕事を表しています。 したがって、理想的な無限多接合太陽電池の限界効率は、赤線で定義された陰影領域と黒線で決定された全光子領域とを比較することによって68.8%であると評価される。 (これは、この方法を「グラフィカルなQE分析」と呼ぶ理由です。)この効率の限界値は、1979年にParrottとVosによって公表された値とそれぞれ一致しますが、それぞれ64%と68.2%です。このレポートと文献の価値。 この小さな違いは、光子束を0eVから0.3096eVに近づける方法が異なるために起こりやすい。 ここでは、光子束を0eVから0.3096eVに光子束を0.31eVで近似した。