ゼロモーメントポイント（Zero moment point ZMP）は、例えばヒューマノイドロボットのための脚式歩行の動力学および制御に関連する概念である。 それは、足と地面との接触における動的反力が水平方向にいかなるモーメントも生じない点、すなわち、水平慣性力と重力力の合計が0（ゼロ）に等しい点を特定する。 この概念は、接触領域が平面であり、足が滑り落ちないように十分に高い摩擦を有すると仮定する。

前書き
この概念は、1968年1月、モスクワの第3回全国大会の理論と応用力学会議でMiomir Vukobratovićによって導入されました。 1970年から1972年の間に制作された次の作品や論文では、それはゼロ・モーメント・ポイントと呼ばれ、世界中に広がります。

モーメントゼロ点は、二足歩行ロボットの運動計画において非常に重要な概念です。 彼らは床との接触点が2つしかなく、動き回ったり、ジャンプしたりすることになっているため、動きは彼らの体全体の力学的安定性に関して計画されなければならない。 これは簡単な作業ではありません。特に、ロボット（胴体）の上体は、ロボットを支持して動かすはずの脚よりも大きな質量と慣性を持っているためです。 これは、倒立振子のバランスを取る問題と比較することができます。

歩行ロボットの軌道は、生成された関節軌道が、所定の安定領域の境界におけるゼロモーメント点の距離によって通常定量化されるロボットの力学的姿勢安定性を確実に保証するように、角運動量方程式を使用して計画される。 ゼロモーメント点の位置は、ロボットの胴の参照質量および慣性の影響を受ける。なぜなら、その運動は、一般に、十分な力学的姿勢安定性を維持するために大きな足首トルクを必要とするからである。

この問題を解決する1つのアプローチは、ロボットの姿勢を安定させるために小さな胴体運動を使用することにある。 しかしながら、ロボットの胴体がその動きを補償するのに必要な足首トルクを減少させるために自然に操舵されるように脚リンクの軌道を定義するためのいくつかの新しい計画方法が開発されている。 脚リンクの軌道計画がうまくいく場合、ゼロモーメントポイントは所定の安定領域から外れず、ロボットの動作は自然な軌道を模倣してより滑らかになる。

ZMP計算
二足歩行ロボットに作用する慣性力および重力の合力は、次式で表される。

どこで  はロボットの総質量、  重力の加速度であり、  質量の中心であり、  重心の加速度です。

いつでもどこでも  次のように定義できます。

どこで  質量中心における角運動量の割合である。
二足歩行ロボットのグローバル運動のニュートン – オイラー方程式は次のように書くことができます：

どこで  Xとの接触力と  任意の点Xに関する接触力に関連する瞬間である。
ニュートン・オイラー方程式は次のように書き直すことができます。

私たちには次のようなことが分かります。

これらの方程式は、接触力と慣性力および重力力が厳密に反対であれば、二足歩行ロボットが動的にバランスしていることを示しています。

軸  モーメントは法線ベクトルに平行である  表面から軸の各点を中心にゼロモーメント点（ZMP）が必然的にこの軸に属している  。 ZMPは軸の交点になります  地面は以下のようになる：

〜と

どこで  ZMPを表します。

重力と慣性力と前述の接触力との間の反対のために、 {\ displaystyle Z}  ポイント（ZMP）は次のように定義できます。

どこで  接触面上の点であり、例えば、質量中心の法線投影である。

コンセプトの歴史
ZMPの概念は、1968年1月にモスクワで開催された第3回連合理学連合（USM）のMiomirVukobratovićによって初めて紹介された。「ゼロ・モーメント・ポイント」という用語は出版された作品に登場した。 次の年の間に。

ZMPへの関心は、ロボット工学者が二足歩行の法則を制御するのに成功した1990年代に始まった。これらの発展を可能にした基本的なモデルは、倒立振子のものである。脚より大きい質量を有する上体は、倒立振子、すなわち移動基部への接続質量からの最初の近似である。ゼロ質量の棒（モデル「カート」）。 問題の質量は、ロボットの重心、ロッドの支持脚、および移動基点を表し、ZMP以外はありません。 このモデルは、重心が一定の高さに留まるHRP-2 1およびHRP-4Cロボットにうまく適用されました。

圧力センターとのリンク
圧力の中心は接触の動的点特性である。 ロボットのすべての加速度に従って定義されるZMPとは異なり、COPは接触面に働く力から定まる局所量である。 しかし、接点が1つしかない場合や、ロボットが水平地面を歩いている場合は、COPとZMPが一致します。

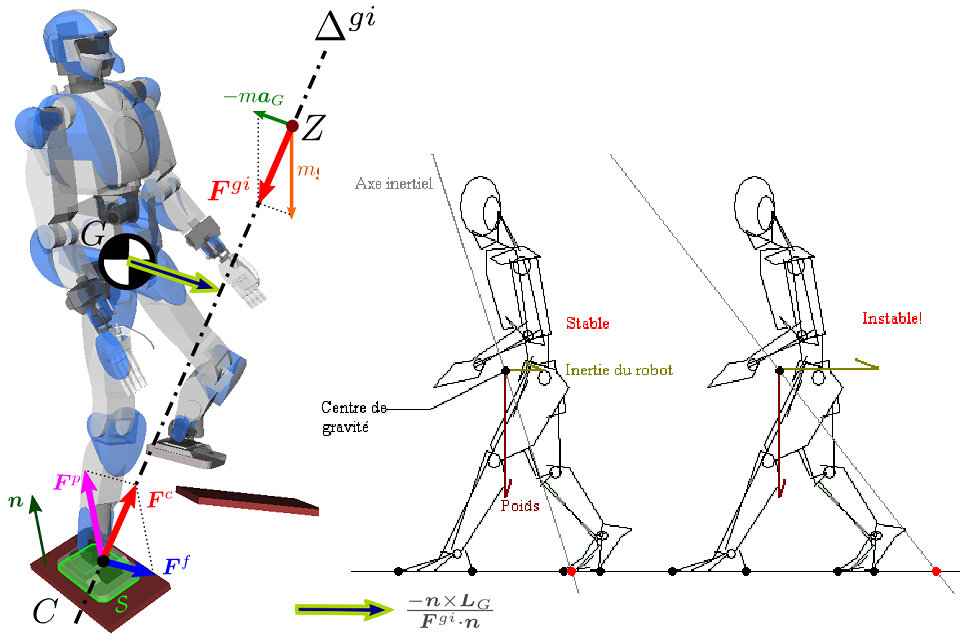
右の図は重心を表しています  、足の右の接触の圧力中心  ZMP  。 ドット  慣性軸上に常に整列している  。 後者は、ロボットがその角運動量を保持しない限り、必ずしも重心を通過するとは限らない（  ）、これは歩行運動における共通の作業仮説である。

平らな地面の特別な場合
表面との接触が壊れない限り、圧力の中心は必然的にロボットと環境との接触面の内部に存在する。 ロボットの2つの足が同じ表面（地面）に接触しているとき、この浮上の表面  サポートのすべてのポイントの凸包です。すなわち、 “2つの足​​の間”に位置するポイントのセットです。 このサーフェスにより、圧力と摩擦、それに関連する圧力中心を定義することができます（詳細は圧力中心を参照）。 COPとZMPが一致するとき、我々は基準を得る：

ノンチルト基準：チルトフリー動作中は、ZMPはリフト面内に位置し、支点の凸包と定義されます。

この基準は、平らな地面上のヒューマノイドロボットの歩行に最も頻繁に用いられる。

アプリケーション
ランプや障害物を移動する際のiRobot PackBotのようなロボットの転倒に対する安定性を評価するために使用できるゼロ・モーメント・ポイントが提案されています。