Цветовое пространство CIE RGB

Цветовое пространство CIE RGB является одним из многих цветовых пространств RGB, отличающимся особым набором монохроматических (одноволновых) основных цветов.
В 1920-х годах У. Дэвид Райт и Джон Гильд независимо провели серию экспериментов по человеческому зрению, которые легли в основу спецификации цветового пространства CIE XYZ. Райт провел трихроматические эксперименты по сопоставлению цветов с десятью наблюдателями. Гильдия фактически провела свои эксперименты с семью наблюдателями.
Эксперименты проводились с использованием кругового расщепленного экрана (двудольное поле) диаметром 2 градуса, что является угловым размером ямки человека. На одной стороне поля проецировался тестовый цвет, а с другой стороны был спроектирован цвет, регулируемый наблюдателем.Регулируемый цвет представлял собой смесь из трех основных цветов, каждая с фиксированной цветностью, но с регулируемой яркостью.
Наблюдатель изменил бы яркость каждого из трех основных лучей до тех пор, пока не будет обнаружено совпадение с тестовым цветом. Не все тестовые цвета могут быть сопоставлены с использованием этой техники. Когда это было так, переменное количество одного из праймериз могло быть добавлено к цвету теста, а совпадение с оставшимися двумя праймерами выполнялось с переменным цветовым пятном. Для этих случаев количество первичного добавленного к тестовому цвету считалось отрицательным. Таким образом, можно охватить весь диапазон восприятия цвета человека. Когда тестовые цвета были монохроматическими, можно было сделать график количества каждого первичного элемента, используемого в зависимости от длины волны тестового цвета. Эти три функции называются функциями согласования цветов для этого конкретного эксперимента.
Хотя эксперименты Райта и Гильдии проводились с использованием различных праймериз с различной интенсивностью, и хотя они использовали несколько разных наблюдателей, все их результаты были обобщены стандартизованными функциями согласования цвета CIE RGB
Функции согласования цветов и праймериз были решены специальной комиссией CIE после значительного обсуждения. Отсеки на коротковолновой и длинноволновой сторонах диаграммы выбираются несколько произвольно; человеческий глаз может действительно видеть свет с длиной волны до 810 нм, но с чувствительностью, которая в тысячи раз ниже, чем для зеленого света. Эти функции согласования цветов определяют так называемый «стандартный наблюдатель CIE 1931». Обратите внимание, что вместо того, чтобы указывать яркость каждого первичного элемента, кривые нормализуются, чтобы иметь под ними постоянную площадь. Эта область привязана к определенному значению, указав, что
Полученные нормализованные функции согласования цветов затем масштабируются в отношении r: g: b 1: 4,5907: 0,0601 для яркости источника и 72.0962: 1.3791: 1 для источника излучения для воспроизведения истинных функций согласования цветов. Предлагая стандартизировать праймериз, CIE установил международную систему объективной цветовой маркировки.
Учитывая эти масштабированные функции согласования цветов, значения тристимула RGB для цвета со спектральным распределением мощности
Все они являются внутренними продуктами и могут рассматриваться как проекция бесконечномерного спектра на трехмерный цвет.
Закон Грассмана
Можно спросить: «Почему возможно, что результаты Райт и Гильдии можно суммировать с использованием разных праймериз и разных интенсивностей от тех, которые на самом деле используются?» Можно также спросить: «Как насчет случая, когда сопоставляемые тестовые цвета не являются монохроматическими?» Ответ на оба этих вопроса заключается в (близкой) линейности восприятия человеческого восприятия. Эта линейность выражается в законе Грассмана.
Пространство CIE RGB можно использовать для определения цветности обычным способом: координаты цветности — r и g, где:
Построение цветового пространства CIE XYZ из данных Wright-Guild
Разработав RGB-модель человеческого зрения с использованием функций соответствия CIE RGB, члены специальной комиссии пожелали разработать еще одно цветовое пространство, которое будет относиться к цветовому пространству CIE RGB. Предполагалось, что закон Грассмана закончен, и новое пространство будет связано с пространством CIE RGB линейным преобразованием. Новое пространство будет определено с точки зрения трех новых функций согласования цветов
Новые функции согласования цветов должны быть везде больше или равны нулю. В 1931 году вычисления выполнялись вручную или с помощью правила скольжения, а определение положительных значений было полезным упрощенным вычислением.
Для белой точки с постоянной энергией требовалось, чтобы x = y = z = 1/3.
В силу определения цветности и требования положительных значений х и у можно видеть, что гамма всех цветов будет находиться внутри треугольника [1, 0], [0, 0], [0, 1] , Требовалось, чтобы гамма заполнила это пространство практически полностью.
Было установлено, что
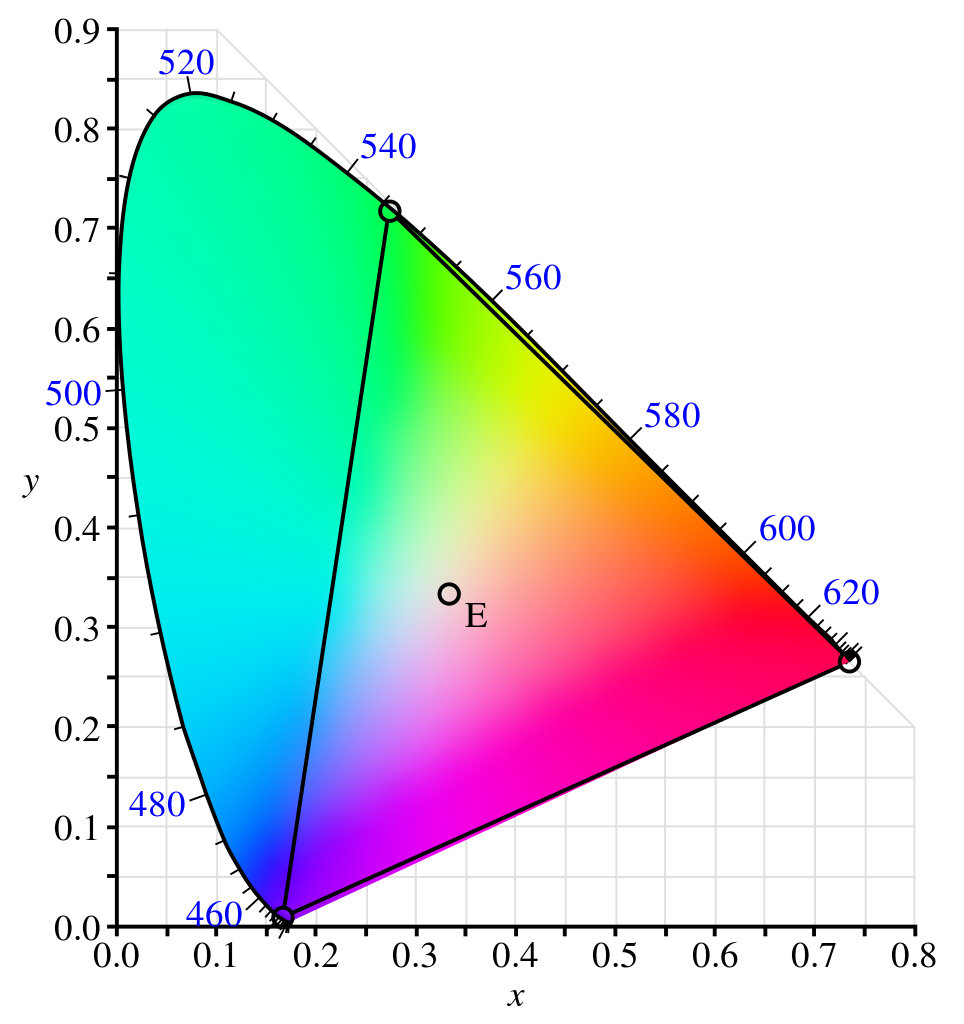
В геометрических терминах выбор нового цветового пространства сводится к выбору нового треугольника в пространстве цветности rg . На рисунке выше справа координаты цветности rg показаны на двух осях черного цвета, а также гамме стандартного наблюдателя 1931 года. Красным цветом обозначены оси цветности CIE xy, которые были определены вышеприведенными требованиями. Требование неотрицательности координат XYZ означает, что треугольник, образованный C r , C g , C b, должен охватывать всю гамму стандартного наблюдателя. Линия, соединяющая C r и C b , фиксируется требованием, чтобы
Числа в матрице преобразования ниже точны, с числом цифр, указанным в стандартах CIE.
Хотя вышеуказанная матрица точно указана в стандартах, в другом направлении используется обратная матрица, которая точно не указана, но примерно равна:
Интегралы функций согласования цвета XYZ должны быть равны по требованию 3 выше, и это задается интегралом функции фотопической световой эффективности согласно требованию 2 выше. Табулированные кривые чувствительности имеют в них определенную произвольность. Форма отдельных кривых чувствительности X, Y и Z может быть измерена с разумной точностью. Однако общая кривая освещенности (которая на самом деле является взвешенной суммой этих трех кривых) является субъективной, поскольку она включает в себя задание испытуемому, имеют ли два источника света одинаковые яркости, даже если они имеют совершенно разные цвета. В то же время относительные величины кривых X, Y и Z произвольны. Кроме того, можно определить допустимое цветовое пространство с кривой чувствительности X, которая имеет удвоенную амплитуду. Это новое цветовое пространство будет иметь другую форму. Кривые чувствительности в цветовых пространствах CIE 1931 и 1964 XYZ масштабируются, чтобы иметь равные площади под кривыми.