
空间网络(Spatial network 有时也是几何图形)是其中顶点或边缘是与几何对象相关联的空间元素的图形,即节点位于配备有某个度量的空间中。 最简单的数学实现是一个格或随机几何图,其中节点在二维平面上随机均匀分布; 如果欧几里德距离小于给定邻域半径,则连接一对节点。 运输和移动网络,互联网,移动电话网络,电网,社交和联系网络以及神经网络都是潜在空间相关的示例,图中的拓扑本身并不包含所有信息。 表征和理解空间网络的结构,弹性和演变对于从城市主义到流行病学等许多不同领域都至关重要。
例子
城市空间网络可以通过将交叉点抽象为节点和街道作为链接来构建,其被称为交通网络。 北京交通作为一个动态网络进行了研究,发现它的渗透特性对发现系统瓶颈很有用。
人们可能会认为“空间地图”是标准地图的负面形象,空间背景的建筑物或墙壁被切开。
表征空间网络
以下几个方面是检验空间网络的一些特征:
平面网络
在许多应用中,例如铁路,道路和其他交通网络,网络被假定为平面。 平面网络在空间网络之外建立了一个重要的群体,但并不是所有的空间网络都是平面的。 事实上,航空公司的乘客网络是一个非平面的例子:世界上所有的机场都通过直航进行连接。
它嵌入太空的方式
有一些网络的例子似乎并没有“直接”嵌入太空。 例如社交网络通过友谊关系连接个人。 但在这种情况下,空间干预了两个人之间的连接概率通常随着它们之间的距离而减小的事实。
Voronoi镶嵌
空间网络可以用Voronoi图来表示,这是一种将空间分割成多个区域的方式。 Voronoi图的对偶图对应于同一组点的Delaunay三角剖分。 Voronoi tessellations对于空间网络来说很有意思,因为它们提供了一个可以比较现实世界网络的自然表示模型。
混合空间和拓扑
检查节点和边缘本身的拓扑结构是表征网络的另一种方法。 经常考虑节点度的分布,关于边的结构,找到最小生成树或泛化,斯坦纳树和相对邻域图是很有用的
格子网络
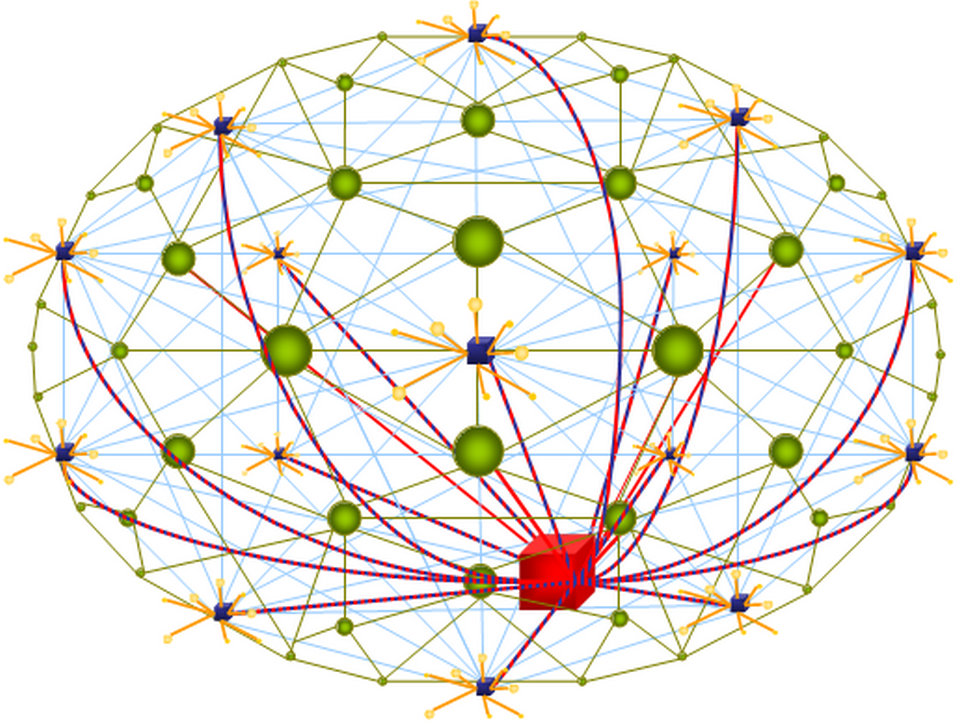
格子网络(见图1)是空间嵌入式网络的有用模型。 已经在这些结构上研究了许多物理现象。 例子包括自发磁化的Ising模型,模拟为随机行走和渗流的扩散现象。 最近为了模拟空间嵌入的相互依存的基础设施的弹性,引入了一个相互依存的格子网络模型(见图2)并进行了分析。 Danziger等人引入了空间复合模型,并由Vaknin等进一步分析。
概率和空间网络
在“真实”世界中,网络的许多方面都不是确定性的 – 随机性扮演着重要的角色。 例如,代表友谊的新链接在社交网络中是随机的。 对随机操作的空间网络进行建模是随之而来的。 在许多情况下,空间泊松过程用于近似空间网络上过程的数据集。 其他随机方面的兴趣是:
泊松线过程
随机几何:Erdős-Rényi图
逾渗理论
从空间句法理论谈起
空间网络的另一个定义来源于空间语法理论。 在涉及大面积开放区域或许多相互关联的路径的复杂空间中,确定空间要素应该是什么是非常困难的。 空间语法的创始人Bill Hillier和Julienne Hanson使用轴线和凸空间作为空间元素。 松散地说,轴线是通过开放空间的“最长视线和通道”,凸空间是可以在空旷空间中绘制的“最大凸多边形”。 这些元素中的每一个都由空间映射的不同区域中的局部边界的几何形状定义。 将空间图分解为完整的相交轴线或重叠凸空间集合,分别产生轴向图或重叠凸图。 存在这些映射的算法定义,并且这允许从任意形状的空间映射到网络的映射适合于以相对明确的方式执行图数学。 轴向地图用于分析城市网络,其中系统通常包含线性区段,而凸面地图更常用于分析建筑平面图,其中空间图案通常更凸出地连接,然而凸面和轴向图也可用于任何情况。
目前,空间语法社群已经开始更好地整合地理信息系统(GIS),并且他们生产的许多软件与市场上可以买到的GIS系统相互链接。
历史
虽然网络和图形已经有很长一段时间了,但是在数学,数学社会学,计算机科学和空间网络方面的许多研究的主题在20世纪70年代在定量地理学中被深入研究。 地理学研究的对象除其他外的地点,活动和个人的流动,还包括网络在时间和空间上的演变。 在这些早期的研究中,大多数重要的问题,例如网络节点的位置,交通网络的演变以及它们与人口和活动密度的相互作用都已得到解决。 另一方面,许多重要的问题仍然不清楚,部分原因是当时缺乏大型网络和更大计算机能力的数据集。 最近,空间网络一直是统计学研究的主题,将概率和随机过程与现实世界中的网络连接起来。