零力矩点

零力矩点(Zero moment point ZMP)是与腿部运动的动力学和控制相关的概念，例如，用于类人机器人。 它指定了脚与地面接触时的动态反作用力在水平方向上不产生任何力矩的点，即水平惯性和重力的总和等于0（零）的点。该概念假设接触区域是平面的并且具有足够高的摩擦力以防止脚滑动。

介绍
这个概念是由Miomir Vukobratović于1968年1月在莫斯科举行的第三届全联合理论与应用力学大会上提出的。 在1970年至1972年间制作的以下作品和论文中，它将被称为零力矩点，并将传播到世界各地。

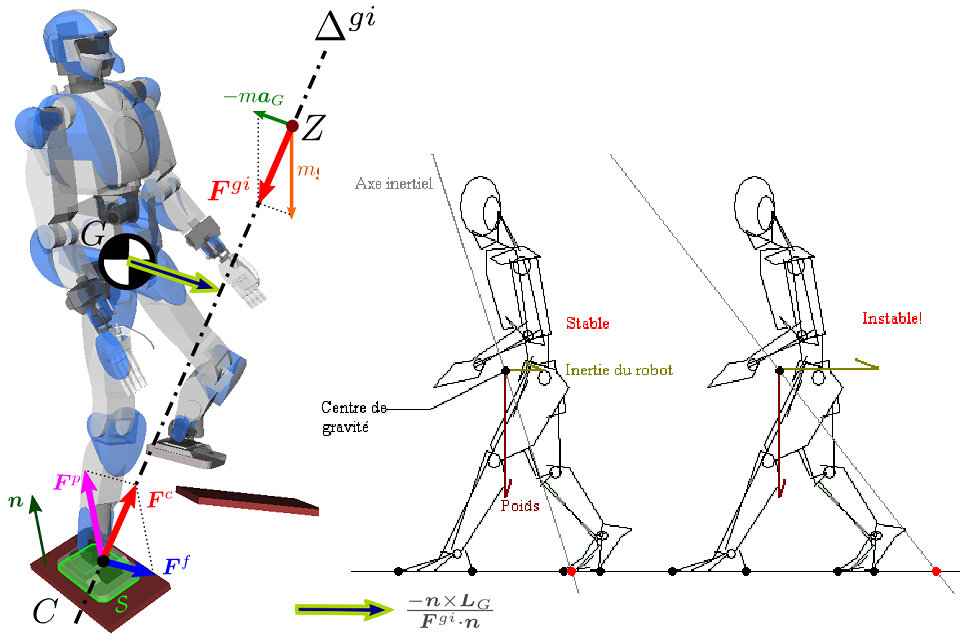
零力矩点是两足机器人运动规划中非常重要的概念。 由于他们只有两个与地板的接触点，他们应该走路，“奔跑”或“跳跃”（在运动环境中），他们的运动必须计划有关他们整个身体的动态稳定性。 这不是一件容易的事，特别是因为机器人的上身（躯干）比支撑和移动机器人的腿具有更大的质量和惯性。这可以与平衡倒立摆的问题进行比较。

使用角动量方程来规划步行机器人的轨迹，以确保所生成的关节轨迹保证机器人的动态姿势稳定性，其通常通过预定稳定区域的边界中的零力矩点的距离来量化。 零力矩点的位置受到机器人躯干的参考质量和惯性的影响，因为其运动通常需要大的踝扭矩以保持令人满意的动态姿势稳定性。

解决该问题的一种方法在于使用小的躯干运动来稳定机器人的姿势。 然而，正在开发一些新的计划方法来定义腿部连杆的轨迹，使得机器人的躯干自然地被操纵以减小补偿其运动所需的脚踝扭矩。 如果腿连杆的轨迹规划很好地成功，那么零力矩点将不会移出预定稳定区域并且机器人的运动将变得更平滑，模仿自然轨迹。

ZMP计算
作用在双足机器人上的惯性力和重力的合力由下式表示：

其中  是机器人的总质量，  是引力的加速度，  是质量和中心  是质心的加速度。

任何一刻的时刻  可以定义为：

其中  是质心的角动量。
双足机器人全局运动的Newton-Euler方程可写为：

其中  是X和X的接触力的结果  是关于任何一点X的接触力的时刻。
牛顿 – 欧拉方程可以改写为：

所以我们更容易看到：

这些方程表明，如果接触力和惯性力与重力完全相反，则双足机器人是动态平衡的。

如果是轴  定义，其中矩与法线向量平行  从表面关于轴的每个点，然后零力矩点（ZMP）必然属于该轴，因为它根据定义沿着矢量定向  。 然后ZMP将成为轴之间的交点  和地面这样：

同

其中  代表ZMP。

由于重力和惯性力与前面提到的接触力之间的对立， {\ displaystyle Z}  point（ZMP）可以定义为：

其中  是接触平面上的一个点，例如质心的正常投影。

这个概念的历史
ZOM的概念最初由MiomirVukobratović在1968年1月在莫斯科举行的理论与应用力学联盟第三次代表大会上提出。“零力矩点”一词出现在已出版的着作中。 在接下来的几年里。

对ZMP的兴趣在20世纪90年代起飞，当时机器人专家成功应用它来控制双足步行的法则。 允许这些发展的基本模型是倒立摆：上半身质量大于腿，行走在于首先近似于倒立摆的运动，也就是说通过倒立摆的连接质量。零质量的杆（模型“CART”）。 所讨论的质量代表机器人的重心，杆支撑腿，移动基点是ZMP。 该模型已成功应用于HRP-2 1和HRP-4C机器人。]其中重心保持恒定高度。

与压力中心联系
压力中心是接触的动态点特征。 与根据机器人的所有加速度定义的ZMP不同，COP是根据施加在接触表面上的力限定的局部量。 但是，当只有一个触点，或者机器人在水平地面上行走时，COP和ZMP重合。

右图代表重心  ，右脚接触的压力中心  以及ZMP  。 点  始终在惯性轴上对齐  。 后者不一定通过重心，除非机器人保持其角动量（  ），这是运动中常见的工作假设。

扁平地面的特殊情况
只要与表面的接触不破裂，压力中心必然位于机器人与环境之间的接触表面内。 当机器人的两脚与同一表面（地面）接触时，这个悬浮表面  是所有支撑点的凸包，也就是说位于“两脚之间”的点集。该表面可以定义压力和摩擦，因此可以定义相关的压力中心（有关详细信息，请参阅压力中心）。COP和ZMP重合，我们得到的标准是：

非倾斜标准：在无倾斜操作期间，ZMP位于升力面内，定义为支点的凸壳。

该标准最常用于平地上的人形机器人的行走。

应用
零弯矩点已被提出作为一种度量标准，可用于评估在航行斜坡和障碍物时对iRobot PackBot等机器人倾翻的稳定性。